trực tâm của tam giác

Trực tâm là gửi gắm điểm của 3 lối cao vô một tam giác.

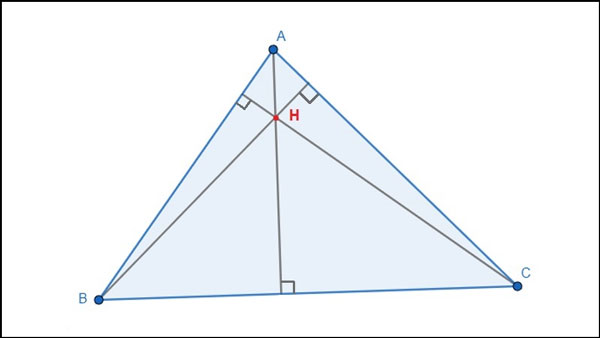
Đường cao vô tam giác là đoạn vuông góc kẻ từ 1 đỉnh cho tới cạnh đối lập. Cạnh đối lập này được gọi là lòng ứng với lối cao. Độ lâu năm của lối cao là khoảng cách thân thiết đỉnh và lòng.

Bạn đang xem: trực tâm của tam giác

• Công thức tính lối cao vô tam giác thông thường, cân nặng, đều, vuông

Cách xác lập trực tâm của tam giác

Trực tâm của tam giác nhọn

Tam giác nhọn ABC sở hữu trực tâm H nằm tại miền vô tam giác.

Trực tâm của tam giác vuông

Trực tâm đó là đỉnh góc vuông. Ví dụ: Tam giác vuông EFG sở hữu trực tâm H trùng với góc vuông E.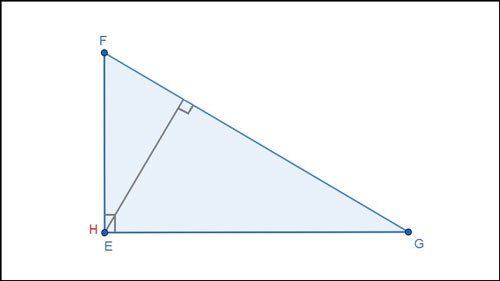

Trực tâm của tam giác tù

Trực tâm của tam giác tù nằm tại miền ngoài tam giác bại liệt. Ví dụ: Tam giác tù BCD sở hữu trực tâm H nằm tại miền ngoài tam giác.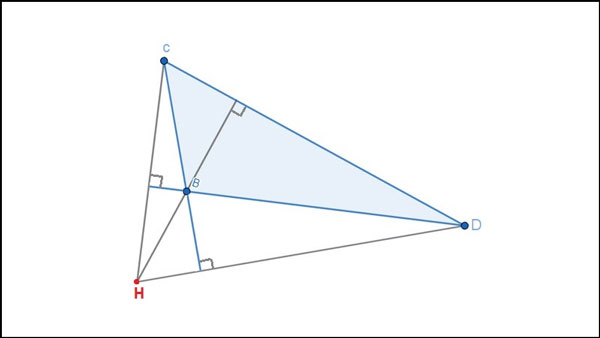

Tính hóa học của trực tâm tam giác

• Khoảng cơ hội kể từ tâm lối tròn trĩnh nước ngoài tiếp tam giác bại liệt cho tới trung điểm cạnh nối nhị đỉnh sót lại bởi vì một nửa khoảng cách từ 1 đỉnh cho tới TT.
• Nếu tam giác đang được nghĩ rằng tam giác cân nặng thì lối cao cũng mặt khác là lối trung tuyến, lối phân giác và lối trung trực của đỉnh tam giác cân nặng bại liệt.
• Trong tam giác đều, trực tâm cũng mặt khác là trọng tâm, tâm lối tròn trĩnh nội tiếp và nước ngoài tiếp của tam giác bại liệt.
• Định lý Carnot: Đường cao tam giác ứng với cùng 1 đỉnh hạn chế lối tròn trĩnh nước ngoài tiếp bên trên điểm loại nhị là đối xứng của TT qua quýt cạnh ứng.

Bài tập luyện về lối trực tâm tam giác

Bài 1:

Cho tam giác ABC ko vuông. Gọi H là trực tâm của chính nó.

Hãy đã cho thấy những lối cao của tam giác HBC. Từ bại liệt hãy đã cho thấy trực tâm của tam giác bại liệt.

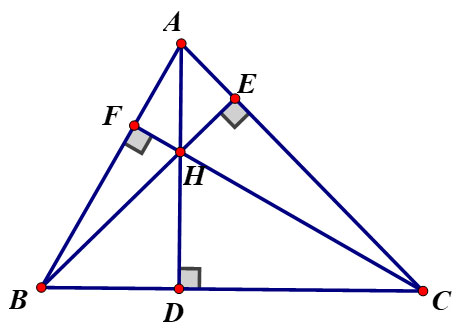
Giải:

Gọi D, E, F là chân những lối vuông góc kẻ kể từ A, B, C của ΔABC.

⇒ AD ⟘ BC, BE ⟘ AC, CF ⟘ AB.

ΔHBC sở hữu :

AD ⊥ BC nên AD là lối cao kể từ H cho tới BC.

BA ⊥ HC bên trên F nên BA là lối cao kể từ B cho tới HC

CA ⊥ BH bên trên E nên CA là lối cao kể từ C cho tới HB.

AD, BA, CA hạn chế nhau bên trên A nên A là trực tâm của ΔHCB.

Bài tập luyện 2:

Xem thêm: in the sustainable agriculture farmers try

Cho △ABC sở hữu những lối cao AD; BE; CF hạn chế nhau bên trên H. I; J thứu tự là trung điểm của AH và BC.

a) Chứng minh: JT⊥EFJT⊥EF

b) Chứng minh: IE⊥JEIE⊥JE

c) Chứng minh: DA là tia phân giác của góc EDF.

d) Gọi P; Q là nhị điểm đối xứng của D qua quýt AB và AC

Chứng minh: P; F; E; Q trực tiếp mặt hàng.

Lời giải:

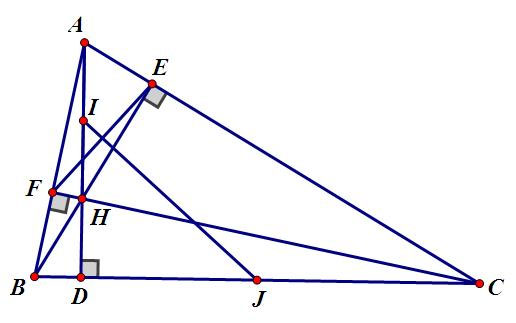
a) Sử dụng đặc thù lối tầm vô tam giác vuông tao có:

FI = 12AH = EIFJ = 12BC = EJFI = 12AH = EIFJ = 12BC = EJ

Vậy IJ là lối trung trực của EF

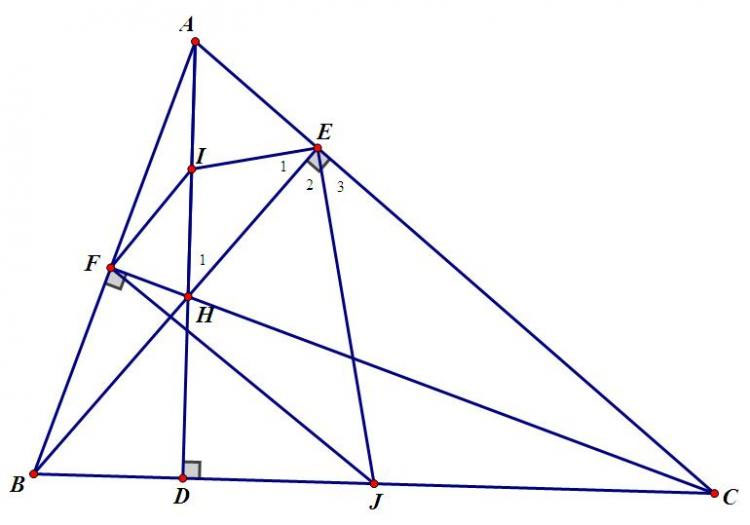
b)

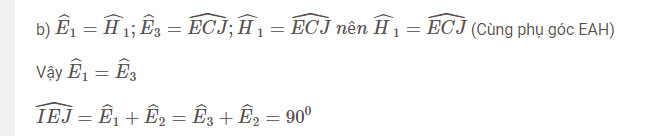
c)Tứ giác BFHD và ABDE nội tiếp (đpcm)

d) H là gửi gắm điểm 3 phân giác của tam giác EFD

Góc PFB = BFD

Xem thêm: công thức tính diện tích hình thang

Góc DFH = EFH

4 góc này nằm trong lại = 2.90 =180 => Phường,E,F trực tiếp hàng

Tương tự động tao sở hữu F, E, Q trực tiếp mặt hàng.