
Ở cấp cho Trung học tập Thương hiệu, những em học viên khối 8 được nghĩ rằng học tập nặng trĩu nhất vì thế những em cần xúc tiếp với thật nhiều dạng toán mới nhất như hằng đẳng thức ở đại số, những hình dạng học tập, đặc điểm và tấp tểnh lý của bọn chúng. Tất cả là nhằm sẵn sàng mang đến lớp 9 và kỳ thi đua lên cấp cho Trung học tập Phổ thông đẫy gay cấn. Trong số những kỹ năng và kiến thức những em được học tập thì kỹ năng và kiến thức về bất phương trình đặc biệt nên được những em chú ý. Bài ghi chép bên dưới đó là cách giải bất phương trình với tương đối đầy đủ lý thuyết quan trọng và bài xích luyện nhằm những em ôn luyện.
1. Bất phương trình một ẩn
– bất phương trình một ẩn là loại bất phương trình đem dạng f(x) > g(x) ( hoặc f(x) < g(x); f(x) ≥ g(x); f(x) ≤ g(x)), nhập tê liệt f(x) và g(x) được gọi là nhì biểu thức của thay đổi x.
Bạn đang xem: cách giải bất phương trình

– Cho số x0 được gọi là nghiệm của bất phương trình f(x) < g(x). Nếu thay cho x0 nhập bất phương trình thì tớ được f(x0) < g(x0) là một trong những xác minh đích thị. Khi giải bất phương trình tớ tìm kiếm ra toàn bộ những nghiệm hoặc hay còn gọi là luyện nghiệm của bất phương trình tê liệt.
– Hai bất phương trình Lúc đem cộng đồng luyện nghiệm thì được gọi là nhì bất phương trình tương tự nhau.
– Phép đổi khác tương tự xẩy ra Lúc thay đổi một bất phương trình trở nên một bất phương trình tương tự.
Một số quy tắc đổi khác phương trình tương tự thông thường người sử dụng cho tới là:
– Chuyển vế : f(x) + h(x) > g(x) ⇔ f(x) > g(x) – h(x)
– Nhân (chia ) :
+ f(x) > g(x) ⇔ f(x) .h(x) > g(x).h(x) nếu như h(x) > 0 với từng x
+ f(x) > g(x) ⇔ f(x) .h(x) < g(x).h(x) nếu như h(x) < 0 với từng x
2. Bất phương trình số 1 một ẩn:
– Bất phương trình một ẩn là loại bất phương trình nhưng mà đem dạng là ax + b > 0 ( hoặc ax + b < 0; ax + b ≥ 0; ax + b ≤ 0) nhập tê liệt số a, số b là những số mang đến trước và a ≠ 0.
– Giải bất phương trình ax + b > 0 (1)
Ta đem (1) ⇔ ax > -b
+ Nếu a > 0 thì (1) ⇔ x > -b/a.
3. Bất phương bậc nhì một ẩn:
– Phương trình bậc nhì một ẩn đem dạng: ax² + bx + c < 0 (hoặc ax² + bx + c > 0, ax² + bx + c ≤ 0, ax² + bx + c ≥ 0)
Trong tê liệt, x được gọi là ẩn; a, b, c là những số thực với a ≠ 0.
– Giải bất phương trình bậc nhì ax² + bx + c < 0 thực ra là mò mẫm những khoảng chừng nhưng mà nhập tê liệt f(x) = ax² + bx + c < 0 nằm trong vết với thông số a (trong tình huống a < 0) hoặc trái khoáy vết với thông số a (trong tình huống a > 0)
Ví dụ 1: Giải bất phương trình sau: 3x² + 2x + 5 > 0
Đặt f(x) = 3x² + 2x + 5, tớ đem f(x) > 0 và a = 3 > 0, vậy nên f(x) luôn luôn dương
Do tê liệt luyện nghiệm của bất phương trình là S = (-∞, +∞)
Ví dụ 2: f(x) = -2x² + 3x + 5, tớ đem a = -2 < 0 và f(x) = 0 ⇔ x = -1 hoặc x = 5/2
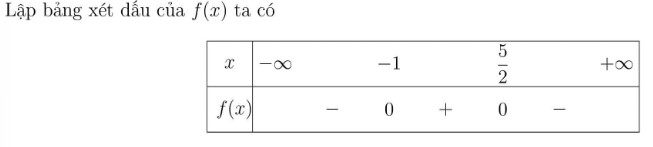
Dựa nhập bảng xét vết tớ đem luyện nghiệm của bất phương trình là: S = (-1;5/2)
4. Tập nghiệm của bất phương trình:
– Số x = 0 gọi là nghiệm của một bất phương trình nào là tê liệt nếu như tớ thay cho x = 0 nhập bất phương trình và thành phẩm tớ được là một trong những bất đẳng thức đích thị.
+ Tập nghiệm của bất phương trình là tụ hợp toàn bộ những nghiệm của bất phương trình tê liệt. Khi tớ đem đề bài xích là giải bất phương trình thì Tức là mò mẫm luyện nghiệm của bất phương trình tê liệt.
+Hai bất phương trình được nghĩ rằng tương tự nhau Lúc nhì bất phương trình đem nằm trong luyện nghiệm.
Ví dụ:
+ Hình 1a màn biểu diễn luyện nghiệm của bất phương trình x > 2
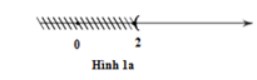
+ Hình 1b màn biểu diễn luyện nghiệm của bất phương trình x ≤ 4
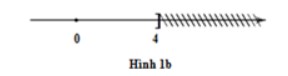
5. Những quy tắc cần thiết nhớ
Quy tắc gửi vế: Khi gửi vế một hạng tử nhập một bất phương trình kể từ vế mặt mày này quý phái vế mặt mày tê liệt thì tớ cần thay đổi vết hạng tử tê liệt.
Quy tắc nhân với 1 số:
Khi nhân nhì vế của một bất phương trình với nằm trong một số trong những không giống số ko, tớ phải:
+ Nếu số này là số dương thì tớ không thay đổi chiều của bất phương trình.
+ Nếu số này là số âm thì tớ cần thay đổi chiều của bất phương trình.
6. Các dạng toán và cách thức giải bất phương trình
Dạng 1: Xác tấp tểnh nghiệm hoặc luyện nghiệm của một bất phương trình và màn biểu diễn nghiệm hoặc luyện nghiệm tê liệt bên trên trục số:
Phương pháp:
Ta dùng những quy tắc sau:
* Quy tắc gửi vế: Khi gửi vế một hạng tử nhập một bất phương trình kể từ vế mặt mày này quý phái vế mặt mày tê liệt thì tớ cần thay đổi vết hạng tử tê liệt.
* Quy tắc nhân với 1 số: Khi nhân nhì vế của một bất phương trình với nằm trong một số trong những không giống số ko, tớ phải:
+ Nếu số này là số dương thì tớ không thay đổi chiều của bất phương trình.
+ Nếu số này là số âm thì tớ cần thay đổi chiều của bất phương trình.
Ngoài đi ra, tớ còn rất có thể dùng hằng đẳng thức hoặc quy đồng hình mẫu số nhằm đổi khác bất phương trình.
Dạng 2: Xác tấp tểnh nhì bất phương trình tương đương:
Phương pháp:
Bất phương trình tương đương: Hai bất phương trình được nghĩ rằng tương tự nhau Lúc nhì bất phương trình đem nằm trong luyện nghiệm.
Dạng 3: Giải bất phương trình bậc nhì.
Phương pháp:
– Cách 1: Biến thay đổi bất phương trình về dạng một vế là tam thức bậc nhì, một vế vì thế 0
– Cách 2: Xét vết vế trái khoáy của tam thức bậc nhì và tóm lại nghiệm.
Dạng 4: Giải bất phương trình tích.
Phương pháp:
– Cách 1: Biến thay đổi bất phương trình về dạng tích những nhị thức số 1 và tam thức bậc nhì.
– Cách 2: Xét vết những nhị thức số 1 và tam thức bậc nhì phía trên và tóm lại nghiệm.
Dạng 5: Giải bất phương trình chứa chấp ẩn ở mẫu
Phương pháp:
– Cách 1: Biến thay đổi bất phương trình đang được mang đến về dạng tích, thương những nhị thức số 1 và tam thức bậc nhì.
– Cách 2: Xét vết những nhị thức số 1 và tam thức bậc nhì phía trên và tóm lại nghiệm.
Chú ý: Cần xem xét ĐK xác lập của bất phương trình.
Dạng 6: Tìm ĐK của thông số nhằm bất phương trình vô nghiệm – đem nghiệm – nghiệm đúng
Phương pháp:
– Sử dụng một số trong những tính chất: Bình phương, căn bậc nhì, độ quý hiếm vô cùng của một biểu thức luôn luôn ko âm.
Dạng 7: Giải hệ bất phương trình bậc hai
Phương pháp:
– Cách 1: Giải từng bất phương trình đem nhập hệ.
– Cách 2: Kết thích hợp nghiệm và tóm lại.
B. BÀI TẬP BẤT PHƯƠNG TRÌNH
I. TRẮC NGHIỆM VỀ BẤT PHƯƠNG TRÌNH
Câu 1: Bất phương trình ax + b > 0 vô nghiệm khi:
A) a ≠ 0 và b = 0
B) a > 0 và b = 0
C) a = 0 và b ≠ 0
D) a = 0 và b ≠ 0
Đáp án đúng chuẩn là: D
Câu 2: Tập nghiệm S của bất phương trình: 5x – 1 ≥ (2x/5) + 3 là?
A) S = R
B) x > 2
C) x < (-5)/2
D) x ≥ 20/23
Đáp án đúng chuẩn là: D
Câu 3: Bất phương trình [(3x + 5)/2] -1 ≤ [(x + 2)/3 + x] đem từng nào nghiệm là nghiệm nguyên vẹn to hơn 10?
A) 4
B) 5
C) 9
D) 10
Đáp án đúng chuẩn là: B
Câu 4: Tập nghiệm S của bất phương trình: (1 – √2)x < √2 – 2 là?
A) x > 2
B) x > √2
C) x < -√2
D) S = R
Đáp án đúng chuẩn là: B
Câu 5: Bất phương trình (2x – 1)(x + 3) – 3x + 1 ≤ (x – 1)(x + 3) + x² – 5 đem luyện nghiệm là?
A) x < -2/3
B) x ≥ -2/3
C) S = R
D) S = Ø
Đáp án đúng chuẩn là: D
Câu 6: Giải bất phương trình: 2x + 4 < 16
A) x > 6
B) x < 6
C) x < 8
D) x > 8
Đáp án đúng chuẩn là: B
Câu 7: Giải bất phương trình: 8x + 4 > 2(x + 5)
A) x > 2
B) x < -1
C) x > -1
D) x > 1
Xem thêm: how old are you trả lời
Đáp án đúng chuẩn là: D
Câu 8: Giải bất phương trình: (x + 2)/3 +3x + 1 > (x – 2)/2
A) x > -6/7
B) x < 6/5
C) x > -16/17
D) x > -6/11
Đáp án đúng chuẩn là: C
Câu 9: Giải bất phương trình: (x + 2)(x – 3) > (2 – x)(6 – x)
A) x > 18/7
B) x > 11/7
C) x < 15/7
D) x < 8/7
Đáp án đúng chuẩn là: A
Câu 10: Tìm m nhằm x = 2 là nghiệm của bất phương trình: mx + 2 < x + 3 + m
A) m = 2
B) m < 3
C) m > 1
D) m < -3
Đáp án đúng chuẩn là: B
Câu 11: Những bất phương trình nào là là bất phương trình một ẩn?
A) 2x – 3 < 0
B) 0.x + 5 > 0
C) 5x – 15 ≥ 0
D) x² > 0
Đáp án đúng chuẩn là: A và C
II. TỰ LUẬN VỀ BẤT PHƯƠNG TRÌNH:
Bài 1: Giải những bất phương trình (theo quy tắc gửi vế)
a) x – 3 > 5
b) 2x ≥ x + 2
c) 2x – 4 < 3x – 2
d) 2,5 – 2x ≤ -x – 3,5
e) 3x – 5 > 2(x – 1) + x
Hướng dẫn giải bài:
a) x – 3 > 5
⇔ x > 5 + 3
⇔ x > 8
Vậy luyện nghiệm của bất phương trình là S = {x|x > 8}
b) 2x ≥ x + 2
⇔ 2x – x ≥ 2
⇔ x ≥ 2
Vậy luyện nghiệm của bất phương trình là: S = {x|x ≥ 2}
c) 2x – 4 < 3x – 2
⇔ 3x – 2x > -4 + 2
⇔ x > -2
Vậy luyện nghiệm của bất phương trình là: S = {x|x > -2}
d) 2,5 – 2x ≤ -x – 3,5
⇔ 2,5 + 3,5 ≤ -x + 2x
⇔ x ≥ 6
Vậy luyện nghiệm của bất phương trình là: S = {x|x ≥ 6}
e) 3x – 5 > 2(x – 1) + x
⇔ 3x – 5 > 2x – x + x
⇔ 3x – 3x > -2 + 5
⇔ 0x > 3
Vậy bất phương trình vô nghiệm
Bài 2: Giải những bất phương trình sau và màn biểu diễn luyện nghiệm của từng bất phương trình bên trên một trục số:
a) 2x – 3 > 3(x – 2)
b) (12x + 1)/12 ≤ (9x + 1)/3 – (8x + 1)/4
c) 5(x – 1) ≤ 6(x – 5/3)
d) (2x – 1)/2 – (x + 1)/6 ≥ (4x – 5)/3
Hướng dẫn giải bài:
a) Ta có:
2x – 3 > 3(x – 2)
⇔ 2x – 3 > 3x – 6
⇔ 6 – 3 > 3x – 2x
⇔ x < 3
Vậy luyện nghiệm của bất phương trình là: S = {x|x < 3}
+ Biểu biểu diễn trục số:
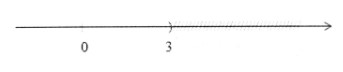
b) Ta có:
(12x + 1)/12 ≤ (9x + 1)/3 – (8x + 1)/4
⇔ (12x + 1)/12 ≤ [4(9x + 1) – 3(8x + 1)]/12
⇔ 12x + 1 ≤ 36x + 4 – 24x – 3
⇔ 12x + 1 ≤ 12x + 1 (luôn đích thị với từng độ quý hiếm x)
Vậy luyện nghiệm của bất phương trình là S = R
+ Biểu biểu diễn bên trên trục số:
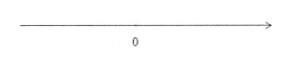
c) tớ có:
5(x – 1) ≤ 6(x – 5/3)
⇔ 5x – 5 ≤ 6x – 10
⇔ 10 – 5 ≤ 6x – 5x
⇔ x ≥ 5
Vậy luyện nghiệm của bất phương trình là: S = {x|x ≥ 5}
+ Biểu biểu diễn trục số:
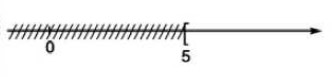
d) Ta có:
(2x – 1)/2 – (x + 1)/6 ≥ (4x – 5)/3
⇔ [3(2x – 1) – (x + 1)]/6 ≥ [2(4x – 5)]/6
⇔ 3(2x – 1) – (x + 1) ≥ 2(4x – 5)
⇔ 6x – 3 – x – 1 ≥ 8x – 10
⇔ 3x ≤ 6
⇔ x ≤ 2
Vậy luyện nghiệm của bất phương trình là: S = {x|x ≤ 2}
+ Biểu biểu diễn trục số:
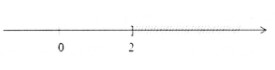
Bài 3: Giải những bất phương trình bậc nhì một ẩn sau:
a) -3x² + 2x + 1 < 0
b) x² + x – 12 < 0
c) 5x² -6√5x + 9 > 0
d) -36x² + 12x -1 ≥ 0
Hướng dẫn giải bài:

Bài 4: Tìm m nhằm từng x ∈ [-1;1] đều là nghiệm của bất phương trình:
3x² – 2(m + 5)x – m² + 2m + 8 ≤ 0
Hướng dẫn giải bài:

Bài ghi chép coi thêm:
Xem thêm: phân tích 10 câu cuối bài vội vàng
Giải phương trình và bất phương trình chứa chấp vết độ quý hiếm tuyệt đối
Trên đó là cách giải bất phương trình nhưng mà HOCMAI mong muốn những em khối 8 xem thêm là rèn luyện theo dõi. Những lý thuyết bên trên đặc biệt cô ứ đọng và được biên soạn thiết thân với sách giáo khoa của cá em vậy nên nó rất thực tiễn biệt và vận dụng được nhập bài xích luyện của những em phía trên lớp. Những bài xích luyện bên trên tuy rằng đặc biệt cơ phiên bản tuy nhiên những em chỉ việc rèn luyện rất nhiều lần là rất có thể ghi lưu giữ được kỹ năng và kiến thức bất phương trình này. Các em cũng nhớ là truy vấn nhập trang web mamnontritueviet.edu.vn để mò mẫm thêm vào cho bản thân nhiều bài học kinh nghiệm hữu dụng nữa nhé!













Bình luận