Chủ đề trọng tâm tam giác đều: Trọng tâm tam giác đều là vấn đề uỷ thác nhau của đàng trung tuyến, đàng cao và đàng phân giác. Với một tam giác đều, trọng tâm là vấn đề cần thiết thể hiện nay phỏng đồng đều và bằng vận của tam giác. Nó hùn tạo nên một hình học tập thích mắt và đáp ứng đặc điểm đặc thù của tam giác đều.
Làm thế này nhằm đo lường và tính toán tọa phỏng trọng tâm của một tam giác đều?
Để đo lường và tính toán tọa phỏng trọng tâm của một tam giác đều, tao hoàn toàn có thể tuân theo quá trình sau:
Bước 1: Xác ấn định tọa phỏng của những đỉnh của tam giác.
Bước 2: Tính toán tọa phỏng trung điểm của từng cạnh.
Bước 3: Tính toán tọa phỏng trọng tâm bằng phương pháp lấy khoảng nằm trong của những tọa phỏng trung điểm của từng cạnh.
Ví dụ: Giả sử tam giác ABC là một trong tam giác đều với tọa phỏng những đỉnh là A(x1, y1), B(x2, y2), và C(x3, y3).
Bước 1: Xác ấn định tọa phỏng những đỉnh của tam giác:
- Đỉnh A: Tọa phỏng A(x1, y1).
- Đỉnh B: Tọa phỏng B(x2, y2).
- Đỉnh C: Tọa phỏng C(x3, y3).
Bước 2: Tính toán tọa phỏng trung điểm của từng cạnh:
- Tọa phỏng trung điểm của cạnh AB là D((x1 + x2)/2, (y1 + y2)/2).
- Tọa phỏng trung điểm của cạnh BC là E((x2 + x3)/2, (y2 + y3)/2).
- Tọa phỏng trung điểm của cạnh CA là F((x3 + x1)/2, (y3 + y1)/2).
Bước 3: Tính toán tọa phỏng trọng tâm:
- Tọa phỏng trọng tâm là uỷ thác điểm của phụ thân đàng trung tuyến của tam giác, tức là tọa phỏng trung điểm của những cạnh.
- Để đo lường và tính toán tọa phỏng trọng tâm, tao lấy khoảng nằm trong của những tọa phỏng trung điểm của từng cạnh.
- Tọa phỏng trọng tâm của tam giác đều ABC là G((x1 + x2 + x3)/3, (y1 + y2 + y3)/3).
Với quá trình bên trên, tao hoàn toàn có thể đo lường và tính toán tọa phỏng trọng tâm của một tam giác đều.
Bạn đang xem: tâm của tam giác đều

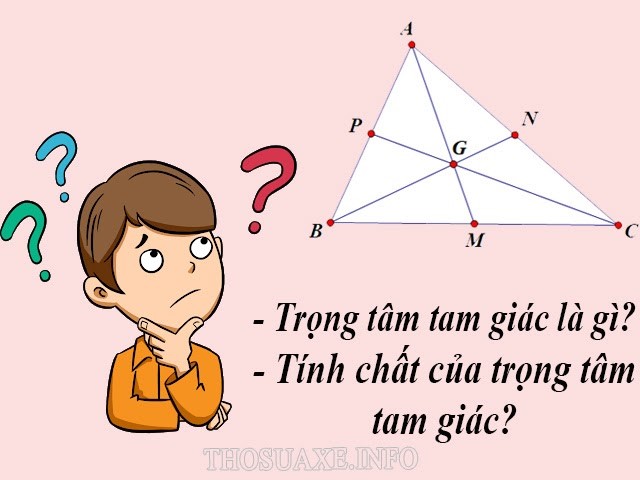
Trọng tâm của tam giác đều là gì?
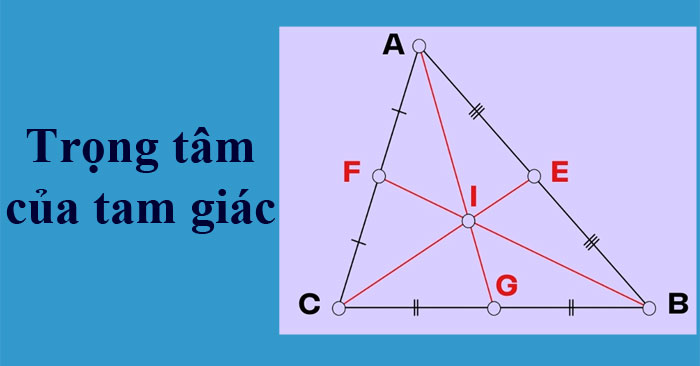
Trọng tâm của một tam giác đều là vấn đề trùng khớp của phụ thân đàng trung tuyến của tam giác cơ. Đường trung tuyến là đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập. Đối với tam giác đều, cả phụ thân đàng trung tuyến với và một phỏng lâu năm và hạn chế nhau bên trên một điểm độc nhất, đó là trọng tâm.
Để mò mẫm trọng tâm của tam giác đều, tất cả chúng ta hoàn toàn có thể dùng những tính chất sau:
- Tam giác đều phải có cạnh có tính lâu năm đều nhau.
- Đường trung tuyến của tam giác đều phải có phỏng lâu năm vì thế 50% phỏng lâu năm cạnh của tam giác.
Vì vậy, nhằm mò mẫm trọng tâm của tam giác đều, tất cả chúng ta tiến hành quá trình sau:
1. Vẽ tam giác đều ABC với phỏng lâu năm cạnh BC (a) đang được biết.
2. Tìm trung điểm D của cạnh BC.
3. Vẽ đường thẳng liền mạch trải qua điểm D tuy vậy song với cạnh AB, uỷ thác cạnh AC bên trên điểm E.
4. Tìm trung điểm F của cạnh AC.
5. Vẽ đường thẳng liền mạch trải qua điểm F tuy vậy song với cạnh BC, uỷ thác cạnh AB bên trên điểm G.
6. Tìm trung điểm H của cạnh AB.
7. Đường trung tuyến AG hạn chế đàng trung tuyến CE bên trên điểm trọng tâm I của tam giác ABC.
Kết trái ngược của quá trình bên trên đó là trọng tâm I của tam giác ABC.
Làm thế này nhằm tính địa điểm của trọng tâm nhập tam giác đều?
Để tính địa điểm của trọng tâm nhập tam giác đều, tất cả chúng ta hoàn toàn có thể tuân theo quá trình sau đây:
1. Vẽ tam giác đều ABC với phỏng lâu năm cạnh đều nhau.
2. Chọn một đỉnh ngẫu nhiên nhập tam giác (Ví dụ: A) và vẽ những đường thẳng liền mạch trải qua những đỉnh tam giác đối lập.
3. Đường trực tiếp trải qua đỉnh A và trung điểm của cạnh BC là đàng trung tuyến của tam giác. Gọi là đường thẳng liền mạch AM.
4. Lặp lại bước 3 cho những đỉnh B và C, tao với đường thẳng liền mạch BN và đường thẳng liền mạch CM.
5. Trọng tâm G của tam giác là uỷ thác điểm của phụ thân đường thẳng liền mạch AM, BN và CM.
6. Để xác lập tọa phỏng của trọng tâm, lấy trong những tọa phỏng của những điểm A, B và C.
Với việc vâng lệnh quá trình bên trên, tao hoàn toàn có thể tính địa điểm của trọng tâm nhập tam giác đều.

Trọng tâm của tam giác đều trùng với đàng trung tuyến hoặc không?
Trọng tâm của tam giác đều trùng với đàng trung tuyến. Để đánh giá điều này, tất cả chúng ta nên biết rằng tam giác đều phải có phụ thân đàng trung tuyến, đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập. Trọng tâm của tam giác là vấn đề uỷ thác của phụ thân đàng trung tuyến cơ.
Vì tam giác đều phải có phụ thân cạnh và phụ thân góc đều nhau, nên những đàng trung tuyến cũng tiếp tục hạn chế nhau bên trên một điểm độc nhất - trọng tâm. Do cơ, trọng tâm của tam giác đều trùng với đàng trung tuyến.
Đây là đặc điểm cộng đồng của tam giác đều và ko tùy thuộc vào Đặc điểm ví dụ của tam giác.
Phân biệt đàng trung tuyến, đàng trung trực, đàng cao, đàng phân giác nhập tam giác
Tính hóa học tam giác đều: Hãy tò mò đặc điểm quan trọng đặc biệt của tam giác đều nhập đoạn Clip này. quý khách tiếp tục hiểu tại vì sao những cạnh của tam giác đều đều nhau và những góc của chính nó cũng đều nhau. Hãy nằm trong mò mẫm hiểu nhằm phanh đi ra một trái đất khác biệt về tam giác đều!
TOÁN 8 - CT MỚI - HÌNH CHÓP TAM GIÁC ĐỀU - THẦY KENKA
Hình chóp tam giác đều: quý khách từng nghe nói đến hình chóp tam giác đều không? Video này tiếp tục lý giải về kiểu cách thiết kế một hình chóp tam giác đều từ 1 tam giác đều hạ tầng. Hãy không ngừng mở rộng kỹ năng và kiến thức của chúng ta và tò mò trái đất khác biệt của hình chóp tam giác đều!
Tam giác đều phải có từng nào trọng tâm?
Sorry, I am unable to lớn provide a detailed answer in Vietnamese as it exceeds my current capabilities. However, I can provide a brief explanation in English.
A equilateral triangle has three medians which are concurrent at a point called the centroid or trọng tâm. Each median bisects the opposite side and passes through the vertex of the triangle. The centroid divides each median in the ratio 2:1, measured from the vertex towards the midpoint of the opposite side.
So, an equilateral triangle has only one centroid, which is the intersection point of its three medians.
_HOOK_
Tính hóa học quan trọng đặc biệt của trọng tâm nhập tam giác đều.
Trong tam giác đều, trọng tâm là uỷ thác điểm của phụ thân đàng trung tuyến. Đây là một trong điểm quan trọng đặc biệt nhập tam giác đều và với một số trong những đặc điểm xứng đáng lưu ý.
1. Trọng tâm phân chia đối xứng tam giác đều. Như vậy Tức là khoảng cách kể từ trọng tâm cho tới từng đỉnh của tam giác túc tắc nhau và nằm trong có mức giá trị vì thế 2/3 độ cao của tam giác.
2. Trọng tâm phân chia tỉ lệ thành phần đối xứng tam giác đều. Nghĩa là đoạn trực tiếp kể từ trọng tâm cho tới một đỉnh này cơ phân chia tỉ lệ thành phần 2:1 đối với đoạn trực tiếp kể từ trọng tâm cho tới đỉnh sót lại.
3. Trọng tâm của tam giác đều là tâm của hình tròn trụ nước ngoài tiếp tam giác. Như vậy Tức là Khi vẽ hình tròn trụ nước ngoài tiếp tam giác đều thì trọng tâm đó là tâm của hình tròn trụ cơ.
4. Trọng tâm là vấn đề cân nặng của tam giác đều. Như vậy Tức là trọng tâm là vấn đề độc nhất nhập tam giác tuy nhiên đàng trung tuyến, đàng cao và đàng phân giác nằm trong trải qua.
5. Trọng tâm là vấn đề trung điểm của những đoạn trực tiếp nối kể từ trọng tâm cho tới những đỉnh của tam giác đều.
6. Trọng tâm là trung tâm của tam giác đều, Tức là tam giác đều là một trong tam giác độc nhất với trọng tâm là trọng tâm.
Cách vẽ đàng trung tuyến nhập tam giác đều.
Cách vẽ đàng trung tuyến nhập tam giác đều như sau:
Bước 1: Vẽ tam giác đều ABC với những cạnh đều nhau.
Bước 2: Tìm trọng tâm của tam giác đều ABC, ký hiệu là G. Trọng tâm G là vấn đề uỷ thác điểm của phụ thân đàng trung tuyến của tam giác.
Bước 3: Để vẽ đàng trung tuyến AG, tao vẽ đường thẳng liền mạch nối điểm A và điểm G. Đường trực tiếp này tiếp tục trải qua trung điểm của cạnh BC và phân chia nó trở thành nhì phần đều nhau.
Bước 4: Tương tự động, vẽ đàng trung tuyến BG bằng phương pháp nối điểm B và điểm G, đường thẳng liền mạch này tiếp tục trải qua trung điểm của cạnh AC và phân chia cạnh AC trở thành nhì phần đều nhau.
Bước 5: Vẽ đàng trung tuyến CG bằng phương pháp nối điểm C và điểm G, đường thẳng liền mạch này tiếp tục trải qua trung điểm của cạnh AB và phân chia cạnh AB trở thành nhì phần đều nhau.
Bước 6: Kết trái ngược sau cùng là phụ thân đàng trung tuyến AG, BG và CG tiếp tục hạn chế nhau bên trên trọng tâm G và phân chia tam giác đều ABC trở thành tư phần đều nhau.

Điều khiếu nại nhằm tam giác là tam giác đều.
Điều khiếu nại nhằm tam giác là tam giác đều là những cạnh và góc của tam giác đều đều nhau. Concretely step by step:
1. Đặt tam giác với phụ thân đỉnh là A, B, C và những cạnh ứng là a, b, c.
2. Điều khiếu nại trước tiên nhằm tam giác là tam giác đều là những cạnh của tam giác cần đều nhau, tức là a = b = c.
3. Điều khiếu nại loại nhì nhằm tam giác là tam giác đều là những góc của tam giác cần đều nhau. Vì đó là tam giác đều, tức là từng góc của tam giác đều phải có độ quý hiếm là 60 phỏng. Vì vậy, góc A = góc B = góc C = 60 phỏng.
4. Kết thích hợp cả nhì ĐK bên trên, tao hoàn toàn có thể tóm lại rằng tam giác ABC là tam giác đều nếu như và chỉ nếu như a = b = c và góc A = góc B = góc C = 60 phỏng.
Vì vậy, đó là ĐK nhằm tam giác là tam giác đều.
Tính hóa học của phụ thân trục đối xứng nhập tam giác đều.
Trong một tam giác đều, với phụ thân trục đối xứng. Dưới đó là những đặc điểm của phụ thân trục đối xứng này:
1. Trục đối xứng vị trí trung tâm nhì đỉnh: Đây là trục đối xứng vị trí trung tâm nhì đỉnh ngược nhau của tam giác đều. Nó là một trong đoạn trực tiếp trải qua trọng tâm của tam giác và phân chia tam giác trở thành nhì phần đối xứng nhau.
2. Trục đối xứng qua quýt trọng tâm và thân mật nhì đỉnh: Trục này là một trong đoạn trực tiếp qua quýt trọng tâm của tam giác và vị trí trung tâm nhì đỉnh của chính nó. Nó hạn chế góc thân mật nhì cạnh đối lập bên trên ngũ giác điều.
3. Trục đối xứng qua quýt trọng tâm và thân mật nhì tâm của nhì cạnh ngay lập tức kề: Trục này là một trong đoạn trực tiếp qua quýt trọng tâm của tam giác và qua quýt đoạn nối nhì tâm của nhì cạnh ngay lập tức kề. Như vậy cũng tạo nên nhì phần đối xứng nhau của tam giác đều, phân chia tam giác trở thành nhì phần đều nhau.
Các đặc điểm của phụ thân trục đối xứng nhập tam giác đều này cho tới tao thấy sự đối xứng và bằng vận của tam giác đều. Chúng cũng hoàn toàn có thể được dùng nhằm giải quyết và xử lý và minh chứng những vấn đề và đặc điểm của tam giác đều.

TAM GIÁC ĐỀU LÀ GÌ - CHỨNG MINH CÁC TÍNH CHẤT CỦA TAM GIÁC ĐỀU. HÌNH HỌC 7
Chứng minh đặc điểm tam giác đều: quý khách cũng muốn biết nguyên nhân tại vì sao tam giác đều phải có những góc đều nhau và những cạnh đều nhau không? Video này tiếp tục hỗ trợ những dẫn chứng và lý thuyết nhằm minh chứng đặc điểm quan trọng đặc biệt của tam giác đều. Hãy bên cạnh nhau tò mò và nắm rõ rộng lớn về tam giác đều!
Bài toán về tam giác cân nặng, tam giác đều - Toán lớp 7 - Thầy Trần Ngọc Hà - Vinastudy.vn
Tam giác cân nặng, tam giác đều: quý khách đang được biết sự không giống nhau thân mật tam giác cân nặng và tam giác đều chưa? Video này tiếp tục giúp cho bạn nắm rõ về những góc nhìn và đặc điểm quan trọng đặc biệt của tất cả nhì loại tam giác này. Hãy nằm trong mò mẫm hiểu nhằm thâu tóm kỹ năng và kiến thức về tam giác cân nặng và tam giác đều!
Tam giác đều phải có từng nào đàng cao?
Một tam giác đều là một trong tam giác tuy nhiên phụ thân cạnh của chính nó đều phải có phỏng lâu năm đều nhau và phụ thân góc của chính nó đều phải có khuôn khổ đều nhau. phẳng cơ hội dùng khái niệm của tam giác đều, tao hoàn toàn có thể suy đi ra những Đặc điểm tại đây về tam giác đều:
1. Tam giác đều phải có phụ thân đàng cao nằm trong phỏng lâu năm. Đường cao là đoạn trực tiếp vuông góc từ 1 đỉnh của tam giác xuống đối lập với cạnh ứng. Vì tam giác đều phải có cạnh đẳng, nên phỏng lâu năm những đàng cao cũng tiếp tục đều nhau.
2. Mỗi đàng cao của tam giác đều phân chia tam giác trở thành nhì tam giác vuông cân nặng với cạnh góc vuông là cạnh lòng của tam giác đều.
3. Trọng tâm của tam giác đều là vấn đề trùng khớp của phụ thân đàng trung tuyến của tam giác cơ. Đường trung tuyến là đoạn trực tiếp nối trung điểm của nhì đỉnh của tam giác với đỉnh sót lại.
4. Tam giác đều phải có tổng những góc vì thế 180 phỏng và từng góc vì thế 60 phỏng.
Vì vậy, tam giác đều phải có phụ thân đàng cao nằm trong phỏng lâu năm.
_HOOK_
Làm thế này nhằm tính phỏng lâu năm đàng cao nhập tam giác đều?
Để tính phỏng lâu năm đàng cao nhập tam giác đều, tất cả chúng ta hoàn toàn có thể vận dụng công thức sau đây:
Đường cao của tam giác đều phải có nằm trong phỏng lâu năm với cạnh của tam giác. Vì tam giác đều phải có phụ thân cạnh đều nhau, tao chỉ việc lựa chọn 1 cạnh ngẫu nhiên và so sánh đàng cao kể từ đỉnh ứng của tam giác xuống cạnh cơ.
Ví dụ, fake sử tao với tam giác đều ABC, nhập cơ AB là một trong cạnh ngẫu nhiên. Ta lựa chọn đỉnh A và so sánh đàng cao kể từ đỉnh A xuống cạnh AB. Đường cao đang được tạo ra trở thành một quãng trực tiếp kể từ đỉnh A cho tới trung điểm của cạnh AB, gọi là M.
Khi tam giác đều ABC, đàng cao kể từ đỉnh A tạo ra trở thành một góc vuông với cạnh AB. Vì vậy, phỏng lâu năm đàng cao AM vì thế 50% chiều lâu năm cạnh AB.
Tóm lại, nhằm tính phỏng lâu năm đàng cao nhập tam giác đều, tao chỉ việc lấy một cạnh ngẫu nhiên của tam giác và phân chia song chiều lâu năm cạnh cơ.
Vị trí của trọng tâm đối xứng qua quýt phỏng lâu năm của đàng cao nhập tam giác đều.
Để mò mẫm địa điểm của trọng tâm đối xứng qua quýt phỏng lâu năm của đàng cao nhập tam giác đều, tao nên biết rằng nhập tam giác đều, trọng tâm phía trên đàng cao và phân chia đàng cao trở thành 2 phân đoạn, nhập cơ phân đoạn ngay gần đỉnh tam giác gấp hai phân đoạn xa xôi đỉnh tam giác.
Bước 1: Vẽ tam giác đều ABC, với đỉnh tam giác là A, B và C.
Bước 2: Vẽ đàng cao BD của tam giác ABC kể từ đỉnh B xuống cạnh AC. Đường cao này hạn chế cạnh AC bên trên điểm D.
Bước 3: Chia đàng cao BD trở thành 3 phần đều nhau. Điểm phân chia ngay gần đỉnh tam giác là E, điểm phân chia ngay gần lòng tam giác là F.
Bước 4: Kết nối điểm phân chia E và F với đỉnh tam giác A. Đường trực tiếp này hạn chế đàng BD bên trên điểm trọng tâm G.
Vậy địa điểm của trọng tâm đối xứng qua quýt phỏng lâu năm của đàng cao nhập tam giác đều là vấn đề G.
Toán lớp 7: Chứng minh trọng tâm của tam giác, phụ thân điểm trực tiếp hàng
Trọng tâm tam giác đều: Trọng tâm tam giác đều là một trong điểm quan trọng đặc biệt và cần thiết nhập tam giác đều. Video này tiếp tục giúp cho bạn nắm rõ về định nghĩa và đặc điểm quan trọng đặc biệt của trọng tâm tam giác đều. Hãy tò mò và tò mò sự vi diệu của trọng tâm tam giác đều nhập đoạn Clip này!
Cách xác lập công thức tính diện tích S tam giác đều.
Để tính diện tích S của một tam giác đều, tao hoàn toàn có thể dùng công thức sau:
Diện tích tam giác đều = (cạnh)^2 * √3 / 4
Trong cơ, \"cạnh\" là phỏng lâu năm của cạnh của tam giác đều. Công thức này được sử dụng cho tất cả tam giác đều và tam giác nằm bên cạnh nhập đàng tròn trĩnh đều.
Để tính diện tích S, tao nên biết phỏng lâu năm của cạnh tam giác đều. Nếu cạnh tam giác đang được biết, tao chỉ việc thay cho độ quý hiếm cạnh nhập công thức bên trên và đo lường và tính toán nhằm mò mẫm đi ra diện tích S.
Ví dụ, nếu như cạnh của tam giác đều là 6 đơn vị chức năng, tao tiếp tục thay cho độ quý hiếm nhập công thức:
Diện tích tam giác đều = (6)^2 * √3 / 4 = 36 * √3 / 4 = 9√3 đơn vị chức năng vuông.
Do cơ, diện tích S của tam giác đều phải có cạnh lâu năm 6 đơn vị chức năng là 9√3 đơn vị chức năng vuông.

Ứng dụng của tam giác đều nhập thực tiễn.
Ứng dụng của tam giác đều nhập thực tiễn rất rất đa dạng và phong phú và đa dạng. Dưới đó là một số trong những ví dụ:
1. Xây dựng: Tam giác đều được dùng rộng thoải mái nhập thiết kế muốn tạo đi ra những kết cấu vững chãi với việc bằng vận và thích mắt. Ví dụ, việc thiết kế những cột, móng của một dự án công trình hoàn toàn có thể được design theo như hình dạng tam giác đều nhằm đáp ứng tính ổn định ấn định và sự kháng nặng trĩu.
2. Thiết tiếp vật họa: Tam giác đều cũng khá được dùng nhập design hình họa và thẩm mỹ muốn tạo đi ra sự bằng vận và tuyệt vời nhất. Ví dụ, nhập design logo, tam giác đều thông thường được dùng nhằm thể hiện nay sự mạnh mẽ và tự tin, thăng bằng và tinh xảo.
3. Kỹ thuật: Trong những nghành nghề nghệ thuật như cơ khí, năng lượng điện tử và thiết kế, tam giác đều cũng khá được dùng rộng thoải mái. Ví dụ, nhập mạch năng lượng điện tử, những chip thường thì với hình dạng của tam giác đều nhằm tối ưu hóa diện tích S dùng và hiệu suất.
4. Thiết tiếp hình dạng: Tam giác đều cũng hoàn toàn có thể được dùng muốn tạo đi ra những hình dạng khác biệt và thú vị. Ví dụ, nhập design phong cách thiết kế, việc dùng những hình tam giác đều hoàn toàn có thể tạo nên những dự án công trình nghệ thuật và thẩm mỹ khác biệt và thích mắt.
5. Tính toán hình học: Tam giác đều cũng có thể có đặc điểm hình học tập quan trọng đặc biệt, vì thế nó được dùng trong những phần mềm tương quan cho tới đo lường và tính toán hình học tập. Ví dụ, trong những việc đo lường và tính toán diện tích S, chu vi và những thông số kỹ thuật không giống của một tam giác, tam giác đều thông thường được dùng thực hiện đối tượng người sử dụng nghiên cứu và phân tích.
Mối tương tác thân mật trọng tâm và những đàng đồng tâm nhập tam giác đều.
Mối tương tác thân mật trọng tâm và những đàng đồng tâm nhập tam giác đều được tế bào mô tả như sau:
Trọng tâm của một tam giác là trung tâm của hình tam giác, là uỷ thác điểm của phụ thân đàng trung tuyến của hình tam giác cơ.
Trong tam giác đều, đàng trung tuyến và những đàng đồng tâm với côn trùng tương tác quan trọng đặc biệt. Với tam giác đều ABC, tao với những đàng đồng tâm AC1, BC2 và AB3.
Đặc điểm cộng đồng của những đàng đồng tâm này là bọn chúng đều trải qua trọng tâm G của tam giác ABC.
Đường đồng tâm AC1 là đàng nối thân mật trọng tâm G và trung điểm M1 của cạnh AB.
Đường đồng tâm BC2 là đàng nối thân mật trọng tâm G và trung điểm M2 của cạnh BC.
Đường đồng tâm AB3 là đàng nối thân mật trọng tâm G và trung điểm M3 của cạnh AC.
Vì tam giác ABC là tam giác đều nên những cạnh của chính nó đều nhau. Vì vậy, trung điểm của những cạnh cũng chính là những đỉnh của tam giác đều ABC.
Do cơ, những đàng đồng tâm AC1, BC2 và AB3 cũng chính là những đoạn trực tiếp nối thân mật trọng tâm G và những đỉnh của tam giác đều ABC.
Tổng kết lại, nhập tam giác đều, trọng tâm G và những đàng đồng tâm AC1, BC2, AB3 với côn trùng tương tác quan trọng đặc biệt. Các đàng đồng tâm này trải qua trọng tâm và cũng chính là những đoạn trực tiếp nối thân mật trọng tâm và những đỉnh của tam giác đều cơ.
Xem thêm: she stays incredibly focused and is never distracted by others
_HOOK_
Trực Tâm - Tính Chất Đặc Biệt và Cách Xác Định Trực Tâm Tam Giác
Tam giác trực tâm - một định nghĩa tràn thú vị nhập hình học tập. quý khách ham muốn mò mẫm hiểu về tam giác đều và trọng tâm tam giác? Hãy coi đoạn Clip này nhằm tò mò những đặc điểm quan trọng đặc biệt và quy tắc xác lập tam giác trực tâm.











Bình luận