Tính thể tích khối tròn trặn xoay là 1 trong trong mỗi đề vấn đề học tập hết sức thú vị được phần mềm vô hình học tập không khí cấp độ trung học tập. Nhờ vô công thức tất cả chúng ta hoàn toàn có thể dễ dàng và đơn giản tính được thể tích vật thể khối tròn trặn xoay xung quanh trục Oy và Ox. Thông qua quýt nội dung bài viết tiếp sau đây, hãy nằm trong Hoàng Hà Mobile thám thính hiểu công thức thể tích khối tròn trặn xoay vô hình học tập không khí và áp dụng vô thực tiễn nhé!
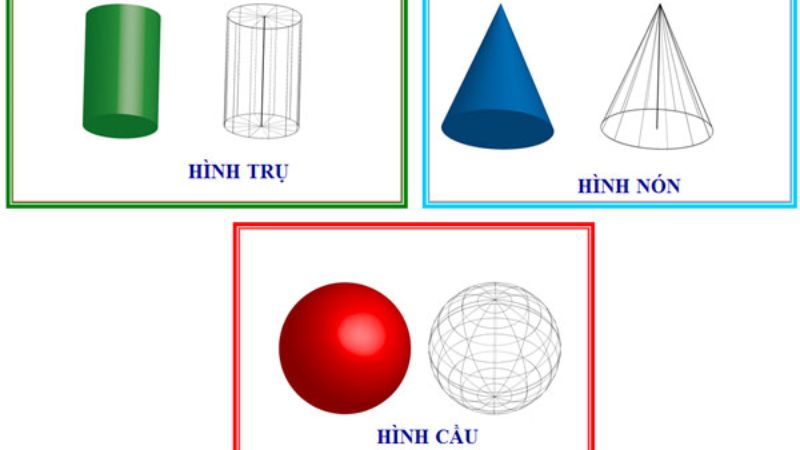
Trước Khi thám thính hiểu về công thức thể tích khối tròn trặn xoay thì bạn phải nắm chắc rõ nét về khái niệm định nghĩa thể tích khối tròn trặn xoay. Trong hình học tập không khí, khối vật thể tròn trặn xoay được khái niệm cơ là 1 trong hình khối được đưa đến trải qua việc xoay xung xung quanh trục Ox hoặc Oy thắt chặt và cố định. Đối với lịch trình hình học tập không khí trung học tập phổ thông, những các bạn sẽ được học tập về thể tích khối nón, khối trụ, khối cầu vật thể tròn trặn xoay.
Bạn đang xem: công thức tính thể tích khối tròn xoay
Công thức thể tích khối tròn trặn xoay là gì?
Công thức thể tích khối tròn trặn xoay dùng để làm tính được toàn cỗ thể tích của vật thể được đưa đến trải qua một đàng cong cù xung xung quanh một trục thắt chặt và cố định. Đây là công thức được dùng vô tình huống này là vật thể hình dạng tròn trặn xoay.
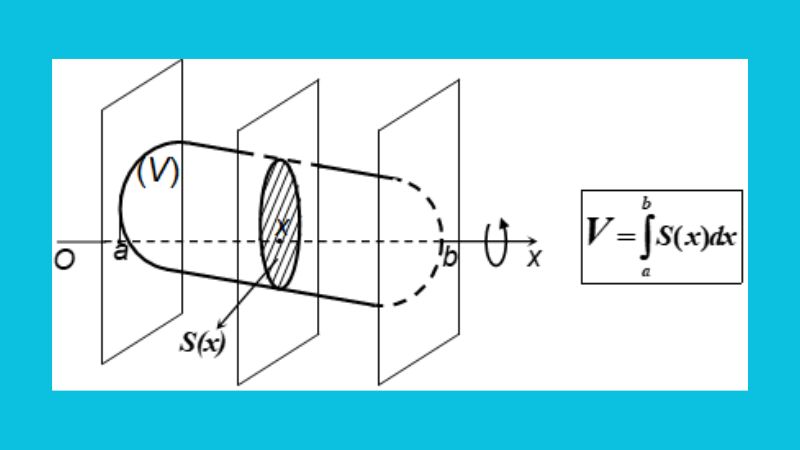
Để hoàn toàn có thể tính được thể tích của khối vật thể tròn trặn xoay thì bạn phải tóm được vấn đề về số đo đàng cao và trục cù. Như vậy, công thức thể tích khối tròn trặn xoay được xác lập cơ là: V = π ∫[a, b] [f(x)]^2 dx. Trong cơ những nhân tố của công thức được xác lập như sau:
- V được khái niệm là thể tích của khối tròn trặn xoay.
- π được khái niệm là hằng số pi, có mức giá trị ngay sát vì chưng 3.14.
- [a,b] được khái niệm là số đo khoảng cách số lượng giới hạn đàng cong, tức là số đo của phần [a,b] phía trên trục Khi vật thể xoay xung xung quanh.
- f(x) được khái niệm là hàm số rất cần phải tế bào mô tả đàng cong đưa đến khối tròn trặn xoay trong vòng phỏng nhiều năm [a,b].

Để hoàn toàn có thể hiểu rộng lớn, bạn cũng có thể xem thêm ví dụ bên dưới đây: Tính thể tích khối tròn trặn xoay xung xung quanh trục Oy sở hữu phương trình Oy= x^2 phía trên khoảng cách kể từ x=0 cho tới x=4. kề dụng công thức bên trên bạn cũng có thể thể hiện được thành quả sau:
V = π ∫[0, 4] (x^2)^2 dx = π ∫[0, 4] x^4 dx
=> V= π [x^5/5] [0, 4] = π * (4^5/5 – 0^5/5) = 12π
Sử dụng công thức tính thể tích vật thể tròn trặn xoay bên trên tớ được thành quả này là 12π.
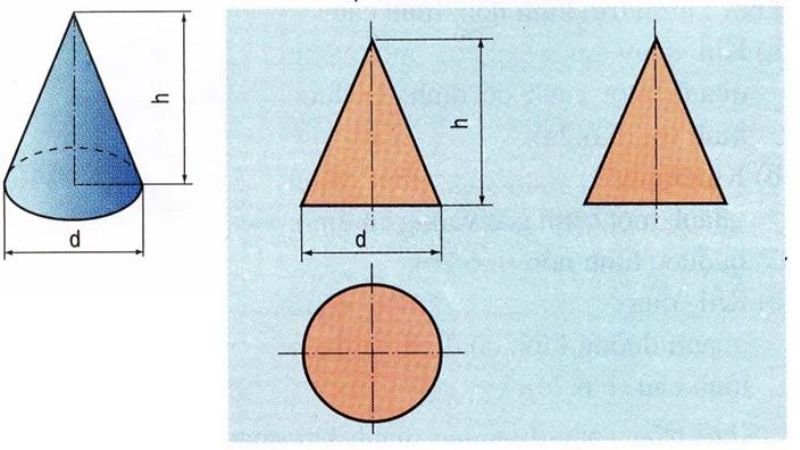
Điểu kiện cần để áp dụng công thức thể tích khối tròn xoay
Để có thể áp dụng được công thức thể tích khối tròn xoay được nêu bên trên cần phải phục vụ điều kiện cần vô toán học. Điều kiện cần đó là khối tròn xoay được tạo đi ra trải qua việc cù xung xung quanh một trục cố định. Có nghĩa phần vật thể này sẽ được một đường cong cố định và xoay xung xung quanh trục nhất định để tạo đi ra hình dạng vật thể tròn xoay. Cụ thể, để áp dụng được khối tròn xoay thì cần phải phục vụ được đầy đủ các vấn đề sau:
- Đường cong xác định cố định được khối vật thể: Phần đường cong này sẽ được xác định trải qua một hảm số biểu diễn đó là y= f(x) hoặc x= g(y). Trong đó f(x) và g)y) được định nghĩa là phương trình hàm số liên trục nằm vô đoạn khoảng cách [a,b] với điều kiện a < b.
- Đoạn [a,b] là khoảng cách phạm vi cần được xác định có vô hàm số của công thức tính thể tích V.
- Trục xung quanh Ox hoặc Oy là ký hiệu bảo hộ biểu diễn cho tới các trục cố định được khối tròn cù xung xung quanh.
Nhìn cộng đồng, để có thể tính được thể tích V của khối tròn xoay thì người mua hàng cần phải xác định phần đường cong được định hình của khối tròn. Cùng với phần phạm vi xác định bao quát trục cố định và đường cong khối tròn cù xung xung quanh. Cuối cùng, áp dụng được công thức thể tích khối tròn xoay dựa vào hàm số đường đoạn cùng phạm vi đã được xác định để tính được thể tích V bám theo đề bài.
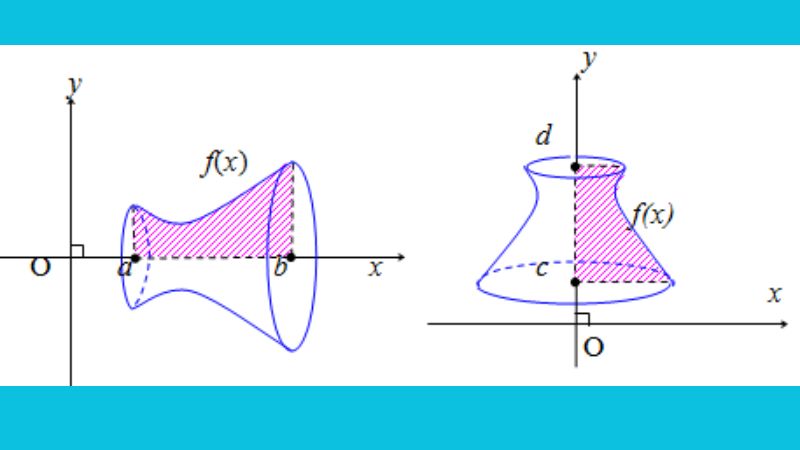
Thể tích khối tròn xoay được tính bám theo công thức nào khác?
Ngoài công thức thể tích khối tròn xoay được nêu bên trên, vật thể tròn xoay còn được tính dựa bám theo công thức khác. Đầu tiên, cần phải xác định được miền (D) mà vật thể xoay xung xung quanh. Khu vực miền này sẽ được giới hạn bởi phần đồ thì biểu diễn bởi phương trình hàm số y= f(x), với đoạn thẳng hàm số x=a, x=b và xoay xung xung quanh trục Ox.
Tiếp bám theo, tiến hành tính khoảng không S được cù xung xung quanh trục Ox của phần khoảng không giới hạn D với công thức đó là S = ∫[a,b] (π[f(x)]^2)dx. Cuối cùng tiến hành tính thể tích V khối tròn xoay bằng cách lấy khoảng không đã tính được nhân với chiều dài L vòng xung quanh trục Ox.
Do đó, công thức tính thể tích khối tròn xoay sẽ được tính bám theo công thức khác đó là: V= S * L. Khi áp dụng công thức này thì người mua hàng sẽ tính được thể tích với vật thể khối tròn xoay một cách chính xác và đơn giản rộng lớn.
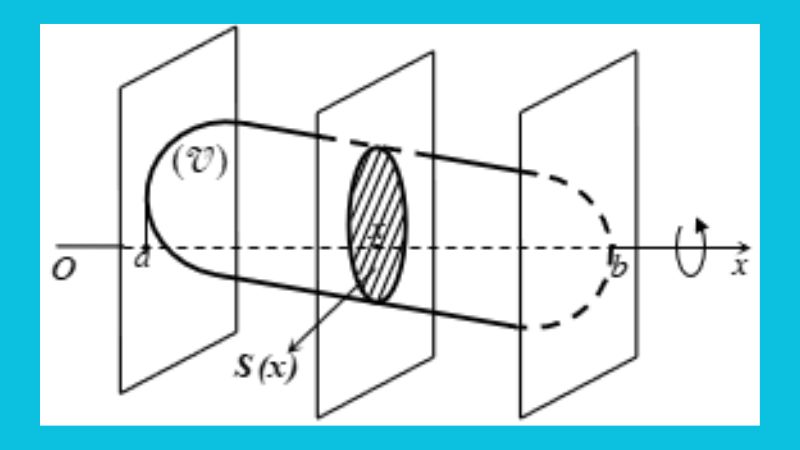
Hướng dẫn tính thể tích khối tròn xoay chi tiết
Sau Khi biết được công thức thể tích khối tròn xoay tuy nhiên nhiều người mua hàng ko nắm được nguồn gốc nghiệp vụ chi tiết tính thể tích khối tròn xoay. Dưới phía trên là nghiệp vụ hướng dẫn chi tiết tính thể tích vật thể tròn xoay như sau:
- Bước 1: Đầu tiên, cần xác định được khu vực vực miền giới hạn của vật thể bởi phương trình biểu diễn hàm số hoặc đường cong được vật thể cù xung xung quanh.
- Bước 2: Tiếp bám theo, xác định phần đoạn thẳng trục Ox được khối tròn cù xung xung quanh. Trục Ox là trục đối xứng của khối tròn.
- Bước 3: Sau đó, tiến hành tính khoảng không S phần miền giới hạn được cù xung xung quanh trục Ox, phía trên là phần khoảng không được tạo đi ra bởi miền giới hạn Khi cù xung xung quanh trục Ox.
- Bước 4: Tiếp bám theo, áp dụng công thức tính thể tích V khối tròn xoay V = π∫(S)dx. Trong đó, π được định nghĩa là số Pi có giá trị xấp xỉ 3.14 và ∫(S)dx là công thức tích phân được xác định phần khoảng không S xung quanh xung xung quanh trục X.
- Bước 5: Cuối cùng thực hiện phép tính tính phân để có thể xác định phần giá trị thể tích V của khối tròn xoay.
Thông qua quýt nghiệp vụ bên trên tớ có thể tính được toàn bộ thể tích của khối tròn xoay cần tính.
Xem thêm: giải pháp bảo vệ môi trường
Vì sao học sinh cần phải nắm rõ công thức thể tích khối tròn xoay?
Công thức thể tích khối tròn trặn xoay là 1 trong trong mỗi công thức cần thiết vô toán hình học tập không khí. Công thức này được dùng nhằm tính thể tích của những vật thể tròn trặn xoay, ví dụ như hình trụ, hình nón, hình cầu,… Việc nắm vững công thức tính thể tích khối tròn trặn xoay sở hữu những ý nghĩa sâu sắc cần thiết sau:
- Giúp học viên nắm rõ thực chất của khối tròn trặn xoay. Công thức tính thể tích khối tròn trặn xoay được suy đi ra kể từ khái niệm của thể tích. Khi học viên nắm vững công thức này, bọn họ tiếp tục nắm chắc quan hệ thân thiện thể tích và những nhân tố của khối tròn trặn xoay, ví dụ như nửa đường kính, độ cao,…
- Giúp học viên giải những bài xích luyện về khối tròn trặn xoay một cơ hội đúng đắn và nhanh gọn lẹ. Các bài xích luyện về khối tròn trặn xoay thông thường có tương đối nhiều dạng không giống nhau, yên cầu học viên nên áp dụng linh động những kiến thức và kỹ năng về hình học tập không khí. Khi nắm vững công thức tính thể tích khối tròn xoay, học viên tiếp tục dễ dàng và đơn giản giải những bài xích luyện này.
- Giúp học viên áp dụng kiến thức và kỹ năng hình học tập không khí vô thực tiễn. Khối tròn trặn xoay là 1 trong loại vật thể thịnh hành vô thực tiễn, ví dụ như lon nước, chai nước khoáng, ly,… Khi nắm vững công thức tính thể tích khối tròn trặn xoay, học viên hoàn toàn có thể đo lường và tính toán thể tích của những vật thể này một cơ hội đúng đắn.
Tầm quan tiền trọng của công thức thể tích khối tròn xoay vô hình học tập và cuộc sống
Việc vận dụng công thức thể tích khối tròn xoay vô hình học tập và cuộc sống rất quan tiền trọng. Bởi vì vô các ngành nghề đều yêu thương mong chờ các kỹ sư cần phải tính toán chính xác được hiệu quả thể tích V của khối tròn xoay.
Trong hình học tập ko gian
Dưới phía trên là tầm quan tiền trọng việc áp dụng hiệu quả công thức tính thể tích V khối tròn xoay vô hình học tập không khí.
- Ứng dụng riêng không liên quan gì đến nhau vô ngành cơ vật lý, nhất là cơ học tập. Ví dụ Khi rất cần phải tính được lượng của một vật thể được tạo ra trở nên trải qua việc cù xung xung quanh một trục. Lúc này tớ rất cần phải tóm được vấn đề thể tích của khối vật thể cơ nhằm tính lượng.
- Trong tình huống về khối tròn trặn xoay thì thể tích là thuật ngữ hết sức cần thiết được dùng nhằm hoàn toàn có thể tính được phần diện tích S mặt phẳng cắt và phần diện tích S của mặt phẳng sở hữu khối hình dạng tròn trặn xoay.
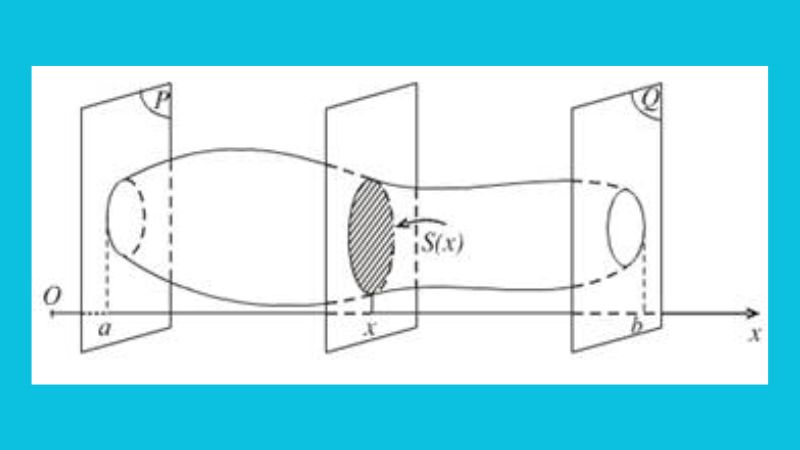
Trong cuộc sống
Dưới phía trên là tầm quan tiền trọng việc áp dụng hiệu quả công thức tính thể tích V khối tròn xoay vô cuộc sống.
- Việc áp dụng công thức tính thể tích giúp hiểu rõ rõ rộng lớn được về tính chất về hình học của khối tròn xoay. Mé cạnh đó, chúng tớ sẽ nắm được phần vị trí với trục cù, kích thước và đặc điểm của khối tròn xoay. Đây là các yếu tố rất quan tiền trọng để áp dụng những thông số khác để tính thể tích vật thể.
- Dễ dàng áp dụng vào các bài toán thực tế với các ngành nghề khác như kỹ thuật, xây dựng, ngành công nghiệp và thiết kế. Khi nắm vững được công thức tính thể tích khối tròn xoay thì sẽ có thể tính toán được phần vật liệu cần sử dụng một cách chính xác, hiệu quả.
- Thể hiện tại đươc khả năng xử lý yếu tố Khi vận dụng được công thức tính thể tích khối tròn xoay. Không chỉ thể hiện tại về mặt mũi kiến thức và kỹ năng về toán học tập mà còn phải đã cho chúng ta thấy được kĩ năng suy nghĩ, xử lý yếu tố và tổ chức triển khai được vấn đề của khách hàng một cơ hội rõ nét.
Không dùng công thức thể tích khối tròn xoay thì có thể tính được không?
Nếu ko sử dụng công thức thể tích khối tròn xoay thì có thể tính được. Tuy nhiên, phương pháp tính tiếp tục phức tạp rộng lớn và yên cầu nhiều bước rộng lớn. Cách tính thể tích vật thể tròn trặn xoay dựa vào nguyên tắc tích phân. Thể tích của vật thể tròn trặn xoay được xem bằng phương pháp phân chia nhỏ vật thể trở nên nhiều phần nhỏ, từng phần là 1 trong hình tròn trụ.
Diện tích của từng phần hình tròn trụ được xem vì chưng công thức πr², vô cơ r là nửa đường kính của hình tròn trụ. Sau cơ, tớ tính tổng diện tích S của toàn bộ những phần hình tròn trụ này bằng phương pháp tính tích phân.
Ví dụ, nhằm tính thể tích của khối nón tròn trặn xoay, tớ hoàn toàn có thể phân chia khối nón trở nên nhiều phần nhỏ, từng phần là 1 trong hình nón nhỏ. Diện tích của từng phần hình nón nhỏ được xem vì chưng công thức πr²h/3, vô cơ r là nửa đường kính lòng của hình nón nhỏ, h là độ cao của hình nón nhỏ. Sau cơ, tớ tính tổng diện tích S của toàn bộ những phần hình nón này bằng phương pháp tính tích phân.
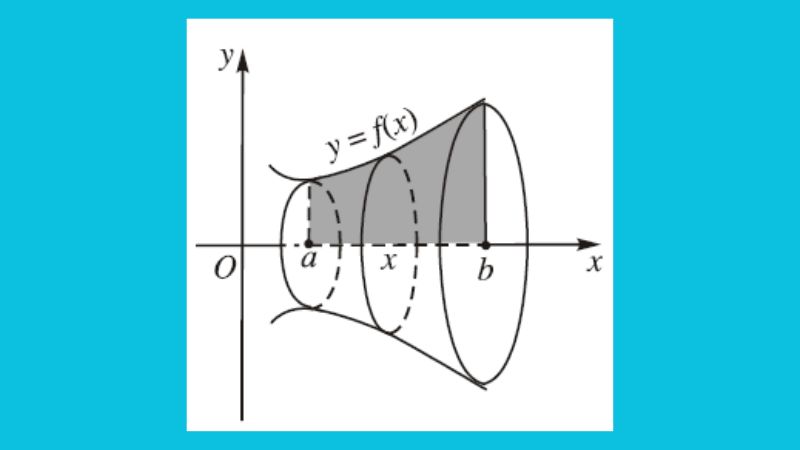
Công thức tích phân tính diện tích S của hình tròn trụ nhỏ là: S = π∫[a,b] (f(x))^2 dx. Trong đó:
- S được định nghĩa là diện tích S của hình tròn trụ nhỏ
- f(x) được định nghĩa là phương trình của hàm số số lượng giới hạn miền D của vật thể tròn trặn xoay
- a và b được định nghĩa là nhị điểm số lượng giới hạn của miền D
Công thức thể tích khối tròn xoay được áp dụng vô lĩnh vực nào?
Đối với công thức thể tích khối tròn xoay được áp dụng vô rất nhiều lĩnh vực sự so sánh vô cuộc sống như:
Lĩnh vực toán học: Đây là một vô những bài toán cực kỳ cơ bản có vô phần hình học không khí lớp 12. Đối tượng bài toán này đó chính là khối tròn được tạo thành bởi việc xoay quanh đường cong đã được xác định. Dạng toán này yêu thương mong chờ học sinh phải nắm vững được kiến thức về phần khoảng không S và thể tích V của khối mong chờ, hình trụ hoặc những hình khác được biểu diễn bởi đường cong.
Lĩnh vực kỹ thuật: Trong lĩnh vực này việc tính được thể tích tròn xoay rất cần thiết. Cụ thể như thiết kế các hệ thống đường ống thì cần tính được chính xác phần thể tích của ống để có thể xác định chính xác phần dung tích chứa chất cần được sử dụng.
Lĩnh vực xây dựng: vô lĩnh vực này phần thể tích V của khối tròn xoay thường được dùng để có thể tính toán chính xác các công trình có hình dạng tron xoay. Ví dụ như các cột xi-măng, ao hồ, hồ đất. Để có thể tiến hành xây dựng chính xác thì cần phải tính được thể tích V của khối tròn xoay,
Xem thêm: chỉ ra biện pháp tu từ
Lĩnh vực thiết kế sản phẩm: Đối với lĩnh vực này, Khi tính được thể tích vật tròn xoay sẽ xác định được phần dung tích một số sản phẩm có hình dạng tròn xoay như ống hút, hũ, lọ, vòng bi,…
Tổng kết
Thông qua quýt nội dung bài viết bên trên, Hoàng Hà Mobile tiếp tục khiến cho bạn tóm được công thức thể tích khối tròn trặn xoay một cơ hội cụ thể. Trong khi, bạn cũng có thể tóm được vai trò của công thức thể tích hình học tập khối tròn trặn xoay và việc vận dụng công thức này vô cơ hội nghành thực tiễn thế nào.
Xem thêm:
- Bảng đơn vị chức năng đo lượng cụ thể nhất – Cách ghi lưu giữ và quy thay đổi chúng
- Số hữu tỉ là gì? Số vô tỉ là gì? Đặc trưng của những số vô Toán học













Bình luận