công thức tính chu vi hình tam giác

Bên cạnh hình vuông vắn, hình chữ nhật thì công thức tính chu vi hình tam giác cũng là 1 trong những trong mỗi kỹ năng toán học tập cần thiết. Và nếu mà độc giả đang được ham muốn gia tăng lại kỹ năng này của bạn dạng thân thích thì nên xem thêm nội dung bài viết sau của Shop chúng tôi nhé!

Hình tam giác là gì?

Trong toán học tập, hình tam giác được khái niệm là 1 trong những hình phẳng phiu 2 chiều đem 3 điểm, 3 đỉnh ko trực tiếp mặt hàng và 3 đoạn trực tiếp nối 3 đỉnh cùng nhau đó là 3 cạnh. Trong toàn bộ những mô hình học tập, tam giác đó là nhiều giác chiếm hữu số cạnh tối thiểu. Không chỉ là 1 trong những nhiều giác lồi, tam giác cũng đó là một nhiều giác đơn. 

Bạn đang xem: công thức tính chu vi hình tam giác

Tùy nằm trong nhập đặc điểm của góc và cạnh thì tam giác được phân thành nhiều loại không giống nhau. Cụ thể như sau: 

Dựa nhập chừng nhiều năm những cạnh

Dựa nhập chừng nhiều năm những cạnh, tam giác được phân thành 3 loại chủ yếu là:

Tam giác thường: Đây là nhiều giác chiếm hữu 3 cạnh với chừng nhiều năm và số đo của những góc không giống nhau. Loại tam giác cơ bạn dạng này cũng rất có thể bao hàm một trong những tam giác quan trọng. 

Tam giác đều: Tam giác đều đó là một hình tam giác cân nặng ở dạng quan trọng tự chiếm hữu 3 cạnh đem số đo đều bằng nhau. Hình tam giác đều phải sở hữu đặc điểm nổi trội là số đo của phụ vương góc đều bằng nhau và đều vày 60o. 

Tam giác cân: Đa giác này chiếm hữu nhì cạnh mặt mày đem số đo đều bằng nhau. Đồng thời, giao phó điểm của nhì cạnh mặt mày cũng đó là đỉnh của tam giác cân nặng. Góc được tạo hình vày đỉnh của tam giác sẽ tiến hành gọi là góc ở đỉnh và góc ở lòng đó là nhì góc sót lại của tam giác. Tam giác cân nặng đem đặc điểm nổi trội là số đo của nhì góc lòng đều bằng nhau. 

Công thức tính chu vi hình tam giác là 1 trong những trong mỗi kỹ năng toán học tập quan lại trọng

Phân loại tam giác theo đòi số đo những góc trong

Dựa nhập số đo những góc nhập, tam giác cũng rất được phân thành một trong những loại là: 

• Tam giác vuông: Tam giác chiếm hữu một góc được tạo ra kể từ nhì cạnh đem số đo góc vày 90o.
• Tam giác tù: Đây đó là tam giác chiếm hữu một góc ngoài đem số đo nhỏ rộng lớn 90o hoặc một góc nhập đem số đo góc to hơn 90o.
• Tam giác nhọn: Đây đó là tam giác chiếm hữu những góc ngoài đem số đo to hơn 90o hoặc những góc nhập đem số đo góc nhỏ rộng lớn 90o.
• Tam giác vuông cân: Loại hình học tập này vừa phải là tam giác cân nặng lại vừa phải là tam giác vuông. Hai cạnh góc vuông nhập tam giác vuông cân nặng tiếp tục đều bằng nhau và góc nhọn sẽ sở hữu số đo vày 45o.

Tính hóa học của hình tam giác 

Sau đó là một trong những những đặc điểm nổi trội của hình tam giác nhưng mà chúng ta có thể tham lam khảo: 

• Trong một hình tam giác, những góc nhập sẽ sở hữu tổng số đo vày 180o.
• Hiệu chừng nhiều năm của nhì cạnh tam giác tiếp tục nhỏ rộng lớn chừng nhiều năm từng cạnh và nhỏ rộng lớn tổng chừng nhiều năm nhì cạnh. 
• Cạnh to hơn nhập một tam giác được xem là cạnh đối lập với góc lớn số 1. 
• Trực tâm của tam giác đó là nút giao nhau của 3 lối cao nhập tam giác. 
• Trọng tâm của tam giác đó là nút giao nhau của 3 lối trung tuyến. 
• Đường trung tuyến đó là đường thẳng liền mạch phân loại tam giác trở nên 2 phần đều bằng nhau về diện tích S. 
• Tâm của lối tròn trĩnh nước ngoài tiếp tam giác đó là nút giao nhau của 3 lối trung trực tam giác. 
• Tâm của lối tròn trĩnh nội tiếp tam giác đó là nút giao nhau của 3 lối phân giác nhập tam giác. 

Trong một hình tam giác, những góc nhập sẽ sở hữu tổng số đo vày 180o

Công thức tính chu vi hình tam giác vuông, cân nặng, đều, vuông cân

Sau đó là tổ hợp những công thức tính chu vi hình tam giác vuông, cân nặng, đều, vuông cân nặng nhưng mà chúng ta nên tham lam khảo:

Công thức tính chu vi hình tam giác thường

là nhiều giác chiếm hữu 3 cạnh với chừng nhiều năm và số đo của những góc không giống nhau. Loại tam giác cơ bạn dạng này cũng rất có thể bao hàm một trong những tam giác quan trọng. Trong toán học tập, công thức tính chu vi hình tam giác thông thường được quy lăm le như sau:

P = a + b + c

Dựa nhập công thức bên trên, tao rất có thể suy rộng lớn ra sức thức tính nửa chu vi hình tam giác như sau:

½ P.. = (a+b+c) : 2

Trong đó:

• P: Ký hiệu chu vi hình tam giác.
• a, b, c: Độ nhiều năm 3 cạnh của hình tam giác. 

Ví dụ: Cho tam giác với chừng nhiều năm những cạnh thứu tự là 3cm , 4 centimet và 5 centimet. Yêu cầu tính chu vi của tam giác tê liệt.

Lời giải: 

• Áp dụng công thức tính chu vi tam giác, tao có: P.. = a + b+ c.
• Theo tài liệu bài bác đi ra thì: a = 3 centimet, b = 4 centimet, c = 5cm
• Chu vi của tam giác tiếp tục cho tới là: P.. = 3 + 4 + 5 = 12 cm

Công thức tính chu vi hình tam giác cân

Tam giác cân nặng là mô hình tam giác chiếm hữu nhì cạnh mặt mày đem số đo đều bằng nhau. Đồng thời, giao phó điểm của nhì cạnh mặt mày cũng đó là đỉnh của tam giác cân nặng. Thế nên, nhằm xác lập được chu vi của hình tam giác cân nặng, các bạn chỉ cần phải biết số đo 2 cạnh và biết đỉnh của tam giác. 

Công thức tính chu vi hình tam giác cân nặng nhập toán học tập được quy lăm le như sau:

P = 2a + c

Xem thêm: phần ảo của số phức

Trong đó:

• P: Ký hiệu chu vi hình tam giác.
• a: Độ nhiều năm 2 cạnh mặt mày của hình tam giác. 
• c: Độ nhiều năm cạnh lòng của hình tam giác.

Ví dụ: Hình tam giác ABC, cân nặng bên trên A với chiều nhiều năm cạnh AB = 7cm, BC = 5cm. Tính chu vi hình tam giác cân nặng.

Bài giải: Dựa nhập công thức tính chu vi tam giác cân nặng, tao đem phương pháp tính P.. = 7 + 7 + 5 = 19cm.

Tam giác cân nặng là mô hình tam giác chiếm hữu nhì cạnh mặt mày đem số đo vày nhau

Công thức tính chu vi hình tam giác đều

Tam giác đều đó là một hình tam giác cân nặng ở dạng quan trọng tự chiếm hữu 3 cạnh đem số đo đều bằng nhau. Hình tam giác đều phải sở hữu đặc điểm nổi trội là số đo của phụ vương góc đều bằng nhau và đều vày 60o.

Công thức tính chu vi hình tam giác đều là: P.. = 3 x a

Trong đó

• P: Ký hiệu chu vi hình tam giác.
• a: Độ nhiều năm 3 cạnh của hình tam giác. 

Ví dụ: Hình tam giác đều ABC, đem chiều nhiều năm cạnh AB = 5cm. Tính chu vi tam giác đều tê liệt. 

Giải: Dựa theo đòi công thức tất cả chúng ta đem phương pháp tính P.. = 5 x 3 = 15cm.

Công thức tính chu vi hình tam giác vuông

Tam giác vuông chiếm hữu một góc được tạo ra kể từ nhì cạnh đem số đo góc vày 90o. Trong toán học tập, công thức tính chu vi hình tam giác vuông là:

P = a + b + c

Trong đó

• P: Ký hiệu chu vi hình tam giác.
• a, b: Độ nhiều năm 2 cạnh của hình tam giác. 
• c: Độ nhiều năm cạnh huyền của hình tam giác.

Ví dụ: Cho hình tam giác vuông ABC có tính nhiều năm cạnh CA = 6cm, cạnh CB = 7cm và cạnh AB = 10cm. Tính chu vi tam giác vuông. 

Giải: Dựa nhập công thức tính tất cả chúng ta đem phương pháp tính P.. = 6 + 7 + 10 = 23cm.

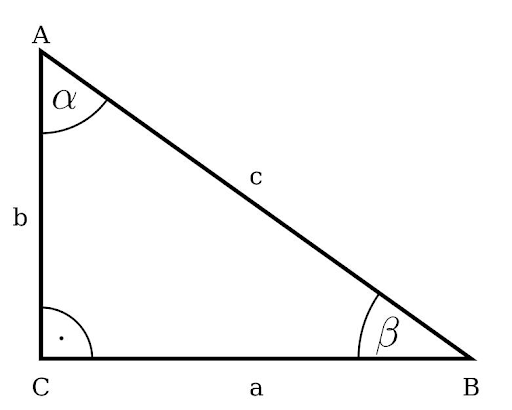
Tam giác vuông chiếm hữu một góc được tạo ra kể từ nhì cạnh đem số đo góc vày 90o

Công thức tính chu vi hình tam giác vuông cân

Loại hình học tập này vừa phải là tam giác cân nặng lại vừa phải là tam giác vuông. Hai cạnh góc vuông nhập tam giác vuông cân nặng tiếp tục đều bằng nhau và góc nhọn sẽ sở hữu số đo vày 45o. Để tính chu vi hình tam giác vuông cân nặng thì tất cả chúng ta cũng vận dụng công thức tính chu vi hình tam giác cân nặng. Cụ thể, tính như sau:

P = 2a + c

Trong đó:

Xem thêm: muốn tính diện tích hình tròn

• P: Ký hiệu chu vi hình tam giác.
• a: Độ nhiều năm 2 cạnh mặt mày của hình tam giác. 
• c: Độ nhiều năm cạnh lòng của hình tam giác.

Ví dụ: Cho tam giác vuông cân nặng ABC với chừng nhiều năm 2 cạnh mặt mày thứu tự là 3, 4 centimet. sành cạnh sót lại của tam giác có tính nhiều năm vội vàng gấp đôi tổng tam giác sót lại. Hãy tính chu vi tam giác tê liệt.

Bài giải:

• Gọi tam giác cần thiết tính chu vi là ABC
• Theo bài bác đi ra tao có: AB = 3cm, AC = 4cm và BC = 2 (AB + AC)
• Như vậy, chiều nhiều năm cạnh sót lại của tam giác là: BC = 2 (AB + AC) = 14 cm
• Chu vi tam giác ABC thời điểm hiện nay tiếp tục bằng: P(ABC) = AB + AC + BC = 3 + 4 + 14 = 19cm

Lời kết

Hy vọng với những share bên trên về công thức tính chu vi hình tam giác, độc giả tiếp tục nhận thêm nhiều kỹ năng hữu ích cho tới bạn dạng thân thích. Từ tê liệt, vận dụng một cơ hội hiệu suất cao nhất nhằm giải những Việc nhập cuộc sống thường ngày hao hao nhập quy trình học hành.