Chủ đề chu vi và diện tích S hình tứ giác: Chu vi và diện tích S hình tứ giác là những thuật ngữ cần thiết nhập toán học tập. phẳng phiu phương pháp tính toán tổng chừng nhiều năm những cạnh, tất cả chúng ta hoàn toàn có thể tìm hiểu rời khỏi chu vi của tứ giác ngẫu nhiên. Tương tự động, diện tích S của tứ giác hoàn toàn có thể được xem vì chưng công thức ½ nhân tích chừng nhiều năm hai tuyến đường chéo cánh. Hiểu rõ rệt về chu vi và diện tích S tứ giác sẽ hỗ trợ tất cả chúng ta vận dụng nó vào thực tiễn và xử lý những vấn đề hình học tập tương quan.
Làm thế nào là nhằm tính chu vi và diện tích S của hình tứ giác?
Để tính chu vi của một hình tứ giác, tớ cần thiết tính tổng những chừng nhiều năm của tứ cạnh của hình cơ. Tức là, chu vi (P) của tứ giác ABCD hoàn toàn có thể tính được vì chưng công thức: Phường = AB + BC + CD + DA.
Để tính diện tích S của một hình tứ giác, tớ cần dùng công thức diện tích S tứ giác ngẫu nhiên. Theo công thức này, diện tích S (S) của tứ giác ABCD hoàn toàn có thể tính được vì chưng nửa tích của chừng nhiều năm lối chéo cánh phân tách cho tới chừng nhiều năm lối cao ứng hoặc nửa tích của tổng phương sai chừng nhiều năm đối của 2 cạnh đối xứng. Tức là:
S = ½ × lối chéo cánh × lối cao (hoặc S = ½ × tổng phương sai chừng nhiều năm đối của 2 cạnh đối xứng).
Do tớ không biết vấn đề cụ thể về hình tứ giác rõ ràng, nên ko thể cung ứng công thức đúng mực nhằm tính diện tích S hình tứ giác. Tuy nhiên, bằng phương pháp vận dụng công thức diện tích S của từng loại tứ giác (ví dụ: hình vuông vắn, hình chữ nhật, hình bình hành, hình thoi, hình trapezoid, hoặc hình tứ giác tù), tớ hoàn toàn có thể tính được diện tích S của từng mô hình tứ giác rõ ràng.
Ví dụ: Đối với hình chữ nhật với chiều nhiều năm (a) và chiều rộng lớn (b), tớ với công thức tính chu vi: Phường = 2(a + b) và công thức tính diện tích S: S = a × b.
Hy vọng vấn đề bên trên mang lại lợi ích cho mình trong các việc tính chu vi và diện tích S của hình tứ giác.
Bạn đang xem: chu vi hình tứ giác


Công thức tính chu vi của một tứ giác là gì?
Công thức tính chu vi của một tứ giác ngẫu nhiên là tổng chừng nhiều năm của tứ cạnh của tứ giác cơ. Để tính chu vi, các bạn cần phải biết chừng nhiều năm của những cạnh. quý khách hoàn toàn có thể tính tổng chừng nhiều năm của những cạnh và thành quả được xem là chu vi của tứ giác cơ. Ví dụ: nếu như chừng nhiều năm những cạnh là AB, BC, CD và DA, công thức tính chu vi là Phường = AB + BC + CD + DA.
Làm thế nào là nhằm tính diện tích S của một tứ giác bất kỳ?
Để tính diện tích S của một tứ giác ngẫu nhiên, tớ hoàn toàn có thể dùng công việc sau:
1. Xác quyết định những thông số kỹ thuật của tứ giác: Thứ nhất, cần thiết xác lập chừng nhiều năm những cạnh của tứ giác. Gọi chừng nhiều năm những cạnh thứu tự là AB, BC, CD và DA.
2. Tính chu vi của tứ giác: Chu vi của một tứ giác vì chưng tổng chừng nhiều năm của những cạnh. Đơn giản nhất là với mọi chừng nhiều năm cạnh lại với nhau: Phường = AB + BC + CD + DA.
3. kề dụng công thức diện tích S tứ giác bất kỳ: Công thức tính diện tích S của một tứ giác ngẫu nhiên là S = một nửa x d1 x d2, nhập cơ d1 và d2 là hai tuyến đường chéo cánh của tứ giác.
4. Xác quyết định chừng nhiều năm lối chéo: Đường chéo cánh của tứ giác là lối nối nhì đỉnh ko kề nhau. Độ nhiều năm của lối chéo cánh hoàn toàn có thể được xem dựa vào quyết định lý Pythagoras hoặc công thức Heron.
5. Tính diện tích S: Sau Lúc có tính nhiều năm lối chéo cánh, vận dụng công thức diện tích S tứ giác ngẫu nhiên, tính độ quý hiếm của (d1 x d2), tiếp sau đó nhân với một nửa nhằm tính diện tích S: S = một nửa x (d1 x d2).
Lưu ý rằng nhằm tính diện tích S của một tứ giác cần phải có chừng nhiều năm của lối chéo cánh, bởi vậy tớ cần phải biết vấn đề về tứ giác cơ hoặc hoàn toàn có thể dùng quyết định lý Pythagoras hoặc công thức Heron nhằm đo lường chừng nhiều năm lối chéo cánh nếu như vấn đề quan trọng được cung ứng.

Chu vi của một tứ giác nào là là vì chưng tổng của chừng nhiều năm tứ cạnh?
Chu vi của một tứ giác ngẫu nhiên là vì chưng tổng của chừng nhiều năm tứ cạnh của chính nó. Để tính chu vi của một tứ giác, các bạn chỉ việc nằm trong tổng chừng nhiều năm của tất cả tứ cạnh lại cùng nhau.
Ví dụ: Nếu các bạn với cùng một tứ giác với chừng nhiều năm những cạnh là a, b, c và d, thì chu vi của tứ giác này sẽ là (a + b + c + d).
Công thức này vận dụng cho tới từng loại tứ giác, bất kể với hay là không những cạnh đều nhau. Nói cách thứ hai, ko quan trọng phải ghi nhận tứ giác là hình vuông vắn, hình chữ nhật hoặc tam giác đều, chỉ cần phải biết chừng nhiều năm của tất cả tứ cạnh là đầy đủ nhằm tính chu vi.
Công thức tính chu vi hình tứ giác ABCD là gì?
Công thức tính chu vi của tứ giác ABCD là Phường = AB + BC + CD + DA. Thứ nhất, bạn phải xác lập chừng nhiều năm những cạnh của tứ giác ABCD. Sau cơ, tiến hành việc với mọi chừng nhiều năm cạnh lại cùng nhau nhằm tính tổng chu vi của tứ giác ABCD.
_HOOK_
Cách tính chu vi hình tứ giác lớp 3 Toán
Với đoạn phim về chu vi hình tứ giác, các bạn sẽ mày mò những công thức và bước tính đúng mực nhằm tìm hiểu chu vi của hình tứ giác một cơ hội dễ dàng và đơn giản. Không chỉ khiến cho bạn thực hiện bài xích luyện, tuy nhiên còn hỗ trợ các bạn nắm rõ kỹ năng Toán lớp
Xem thêm: công thức quá khứ hoàn thành
Công thức tính diện tích S hình tứ giác 4 cạnh
Nhờ đoạn phim về diện tích S hình tứ giác, các bạn sẽ làm rõ rộng lớn về kiểu cách tính diện tích S của hình tứ giác và được trình diễn một cơ hội rõ nét, rõ ràng. Đây thiệt sự là một trong những công thức giản dị và hữu ích cho những vấn đề Toán lớp 6 của người sử dụng.
Nếu chu vi hình tứ giác ABCD là 73cm và AB = 52cm, hãy tính chừng nhiều năm của cạnh sót lại.
Để tính chừng nhiều năm của cạnh sót lại của hình tứ giác ABCD, tớ dùng công thức tính chu vi của tứ giác: Phường = AB + BC + CD + DA.
Theo câu đề bài xích, chu vi hình tứ giác ABCD là 73cm và AB = 52cm.
Như vậy tớ có: 73cm = 52cm + BC + CD + DA.
Ta cần thiết tính chừng nhiều năm của cạnh sót lại, tức là cần thiết tìm hiểu độ quý hiếm của BC + CD + DA.
Để tìm ra độ quý hiếm này, tớ hoàn toàn có thể tiến hành luật lệ tính dư như sau:
BC + CD + DA = chu vi - AB
BC + CD + DA = 73cm - 52cm
BC + CD + DA = 21cm
Qua cơ, tớ tìm ra độ quý hiếm của cạnh sót lại của hình tứ giác ABCD là 21cm.
Làm thế nào là nhằm tính diện tích S hình tứ giác?
Để tính diện tích S của một hình tứ giác ngẫu nhiên, tất cả chúng ta hoàn toàn có thể dùng những cách thức sau đây:
Bước 1: Xác quyết định những vấn đề quan trọng về những cạnh và góc của hình tứ giác. Đây hoàn toàn có thể là chừng nhiều năm những cạnh, chừng nhiều năm lối chéo cánh, góc Một trong những cạnh, hoặc ngẫu nhiên vấn đề không giống tương quan cho tới hình tứ giác.
Bước 2: Sử dụng công thức tính diện tích S hình tứ giác ứng với mô hình tiếp tục cho tới. Có nhiều mô hình tứ giác, ví như hình vuông vắn, hình chữ nhật, hình bình hành, trapezoid, hình thoi, và hình tứ giác ngẫu nhiên. Mỗi loại với công thức tính diện tích S riêng rẽ.
Ví dụ: Đối với cùng một hình tứ giác ngẫu nhiên, công thức tính diện tích S là:
Diện tích = ½ x lối chéo cánh AC x lối chéo cánh BD x sin(AB,CD)
Trong cơ, AC và BD thứu tự là lối chéo cánh của hình tứ giác và AB, CD là góc tạo nên vì chưng hai tuyến đường chéo cánh. Hãy ghi nhớ rằng góc này được xem bám theo đơn vị chức năng radian, ko nên chừng.
Bước 3: Sử dụng những vấn đề tiếp tục biết về những cạnh và góc của hình tứ giác, vận dụng công thức tính diện tích S kể từ bước 2 nhằm đo lường và tìm hiểu rời khỏi độ quý hiếm diện tích S.
Ví dụ: Giả sử tất cả chúng ta hiểu được lối chéo cánh AC có tính nhiều năm 6 centimet, lối chéo cánh BD có tính nhiều năm 8 centimet và góc thân thích hai tuyến đường chéo cánh là 60 chừng. kề dụng công thức, tớ có:
Diện tích = ½ x 6 centimet x 8 centimet x sin(60 độ) = 24 cm²
Vậy diện tích S của hình tứ giác nhập tình huống này là 24 cm².
Nếu hình tứ giác với loại đặc biệt quan trọng như hình vuông vắn, hình chữ nhật, hoặc hình bình hành, thì hoàn toàn có thể dùng công thức riêng rẽ của từng loại nhằm tính diện tích S một cơ hội dễ dàng và đơn giản rộng lớn.
Hơn nữa, nếu như vấn đề về hình tứ giác ko cung ứng đầy đủ, tất cả chúng ta cần thiết tìm hiểu hiểu thêm thắt vấn đề hoặc dùng cách thức không giống nhằm tính diện tích S.
Tại sao diện tích S của một tứ giác vì chưng 50% tích những lối chéo?
Diện tích của tứ giác vì chưng 50% tích những lối chéo cánh tự lối chéo cánh phân tách tứ giác trở nên nhì tam giác đều nhau. Ta hoàn toàn có thể chứng tỏ điều này như sau:
Gọi ABCD là một trong những tứ giác, AC và BD là hai tuyến đường chéo cánh của tứ giác.
Ta tiếp tục chứng tỏ tổng diện tích S nhì tam giác ABC và ACD vì chưng diện tích S của tứ giác ABCD.
Để chứng tỏ điều bên trên, tớ tiếp tục dùng công thức diện tích S của một tam giác vuông. Gọi h là độ cao của tam giác ABC và d là độ cao của tam giác ACD. Ta có:
Diện tích tam giác ABC = một nửa * AB * h.
Diện tích tam giác ACD = một nửa * AD * d.
Vì tứ giác ABCD là một trong những tứ giác đều nhau, nên AB = AD và h = d.
Do cơ,
Diện tích tam giác ABC = một nửa * AB * h = một nửa * AB * d.
Diện tích tam giác ACD = một nửa * AD * d = một nửa * AB * d.
Tổng diện tích S nhì tam giác ABC và ACD là:
Diện tích tứ giác ABCD = Diện tích tam giác ABC + Diện tích tam giác ACD
= một nửa * AB * d + một nửa * AB * d
= AB * d.
Vì d = h, nên Diện tích tứ giác ABCD = AB * h.
Vậy, tất cả chúng ta tiếp tục chứng tỏ rằng diện tích S của một tứ giác vì chưng 50% tích những lối chéo cánh (Diện tích tứ giác ABCD = AB * h = một nửa * AB * d).
Công thức tính diện tích S của 7 hình khiến cho bạn học tập xuất sắc Toán
Bạn đang được tìm hiểu tìm tòi một công thức giản dị nhằm tính diện tích? Video này tiếp tục cung ứng cho mình công thức tính diện tích S hình tứ giác một cơ hội cụ thể và dễ dàng nắm bắt. Hãy bám theo dõi nhằm nắm rõ kỹ năng và vận dụng nhập những bài xích luyện Toán lớp 6 của người sử dụng.
Một ví dụ rõ ràng về kiểu cách vận dụng công thức tính diện tích S của một tứ giác.
Để tính diện tích S của một tứ giác ngẫu nhiên, tất cả chúng ta hoàn toàn có thể dùng công thức sau: Diện tích tứ giác = 0.5 * (đường chéo cánh chủ yếu 1 * lối chéo cánh chủ yếu 2).
Ví dụ, fake sử tất cả chúng ta với cùng một tứ giác ABCD với lối chéo cánh chủ yếu 1 có tính nhiều năm AB = 6 centimet và lối chéo cánh chủ yếu 2 có tính nhiều năm CD = 8 centimet. Chúng tớ hoàn toàn có thể tính diện tích S của tứ giác này như sau:
Diện tích tứ giác ABCD = 0.5 * (AB * CD)
= 0.5 * (6 centimet * 8 cm)
= 0.5 * 48 cm²
= 24 cm².
Vậy diện tích S của tứ giác ABCD là 24 cm².
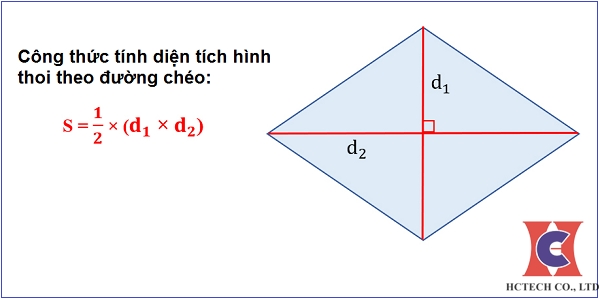
Tính diện tích S của một hình thoi lúc biết cạnh và lối chéo cánh của nó?
Để tính diện tích S của một hình thoi lúc biết cạnh và lối chéo cánh của chính nó, tớ hoàn toàn có thể tuân theo công việc sau:
Bước 1: Xác quyết định những độ quý hiếm tiếp tục biết.
- Gọi a là cạnh của hình thoi.
- Gọi d là lối chéo cánh của hình thoi.
Bước 2: kề dụng công thức tính diện tích S hình thoi.
Diện tích của một hình thoi hoàn toàn có thể được xem vì chưng công thức: Diện tích = (1/2) × cạnh × lối chéo cánh.
Vậy, diện tích S của hình thoi là: Diện tích = (1/2) × a × d.
Lưu ý: Đơn vị chiều nhiều năm của cạnh và lối chéo cánh nên được giống hệt, ví như centimet, m, hoặc milimet.
Ví dụ: Nếu cạnh của hình thoi là 6 centimet và lối chéo cánh là 10 centimet, tớ hoàn toàn có thể tính diện tích S như sau:
Diện tích = (1/2) × 6 centimet × 10 cm
Diện tích = 30 cm²
Vậy diện tích S của hình thoi nhập ví dụ này là 30 cm².
_HOOK_
Toán lớp 6 - Kết nối | Bài 20: Chu vi và diện tích S tứ giác - trang 91 - 94
Bạn đang được học tập môn Toán lớp 6 và ham muốn tìm hiểu hiểu thêm thắt về những định nghĩa và công thức cơ bản? Video này tiếp tục khiến cho bạn nắm rõ kỹ năng và cung ứng những vấn đề thực tiễn nhằm vận dụng những gì tiếp tục học tập. Hãy nằm trong coi và nâng lên trình độ chuyên môn Toán của người sử dụng.
Đang xử lý...













Bình luận