Bài tập luyện rút gọn gàng biểu thức ở lớp 9 thông thường kèm theo với dạng toán phụ. Đó là những dạng:
Dạng 1: Rút gọn gàng biểu thức cơ bản
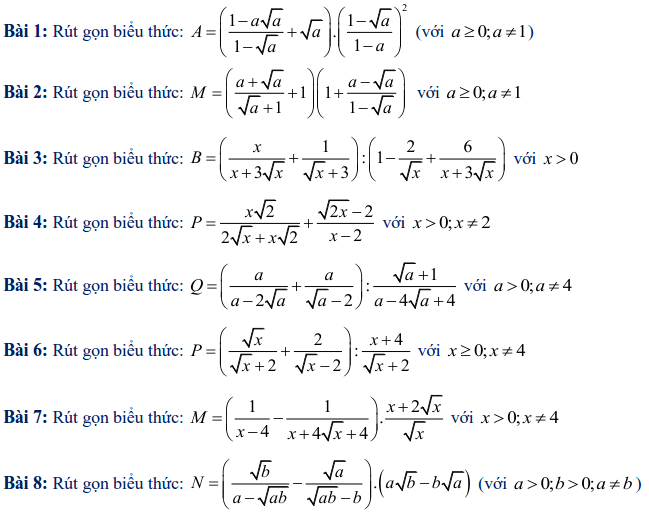
Bạn đang xem: bài tập rút gọn biểu thức lớp 9
Dạng 2: Rút gọn gàng biểu thức và tính độ quý hiếm của biểu thức Lúc mang đến độ quý hiếm của ẩn
Các bước thực hiện:
– Rút gọn gàng, xem xét ĐK của biểu thức
– Rút gọn gàng độ quý hiếm của vươn lên là nếu như cần
– Thay vô biểu thức rút gọn
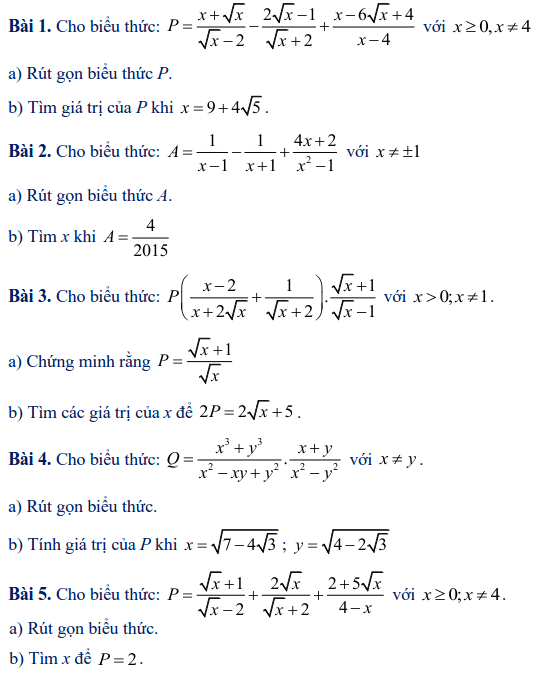
Dạng 3: Rút gọn gàng biểu thức và dò xét x nhằm biểu thức rút gọn gàng đạt độ quý hiếm nguyên
– Rút gọn gàng biểu thức
– Lấy tử phân tách mang đến kiểu tách biểu thức trở thành tổng của một vài nguyên vẹn và một biểu thức đem tử là một vài nguyên
– Trong biểu thức mới nhất tạo ra trở thành, tao mang đến kiểu là những ước nguyên vẹn của tử nhằm suy rời khỏi x.

Dạng 4: Rút gọn gàng biểu thức và dò xét x nhằm biểu thức thỏa vì chưng hoặc to hơn (nhỏ hơn) một vài mang đến trước
– Rút gọn
– Cho biểu thức rút gọn gàng thỏa ĐK tao được phương trình hoặc bất phương trình, xem xét ĐK của ẩn vô Việc.
Xem thêm: công thức tính thể tích hình chóp
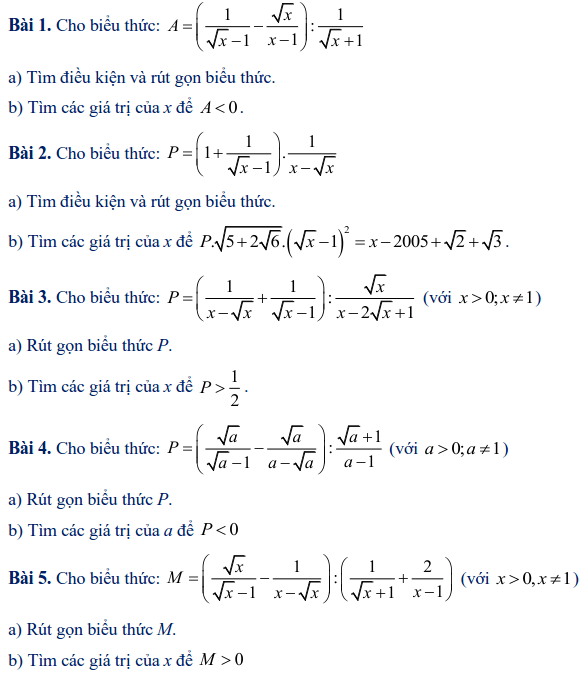
Dạng 5: Rút gọn gàng biểu thức và dò xét x nhằm biểu thức đạt độ quý hiếm lớn số 1 (GTLN), độ quý hiếm nhỏ nhất (GTNN)
– Rút gọn
– Biến thay đổi biểu thức (BT) về dạng:
+ Số ko âm + hằng số ⇒ GTNN.
VD: A2 + m ≥ m. Khi cơ GTNN của biểu thức vì chưng m xẩy ra Lúc và chỉ Lúc A = 0.
+ Hằng số – số ko âm ⇒ GTLN.
VD: M – A2 ≤ M. Khi cơ GTLN của biểu thức vì chưng M xẩy ra Lúc và chỉ Lúc A = 0.
+ Sử dụng bất đẳng thức Cô-si: Cho nhì số dương a và b, tao có:
$a+b \geq 2 \sqrt{a b}$. Dấu “=” xẩy ra Lúc và chỉ khi a = b.
+ |A| + |B| ≥ |A + B|
Xem thêm: how old are you trả lời
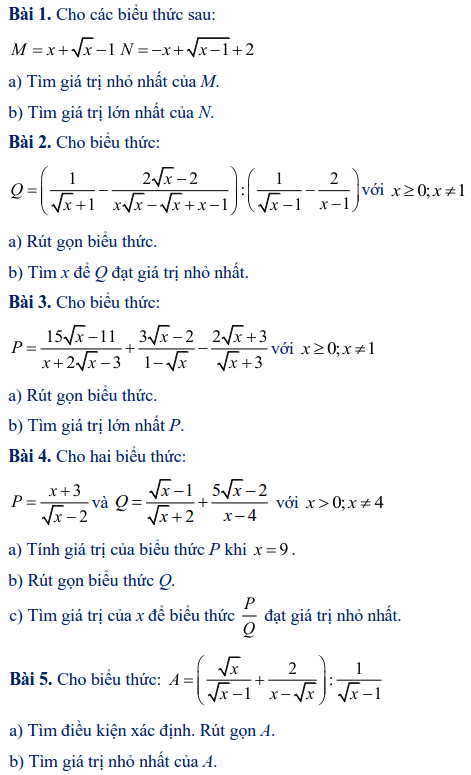
Dạng 6: Rút gọn gàng biểu thức và những Việc khác

*Download tệp tin Bài tập luyện rút gọn gàng biểu thức lớp 9 theo đuổi từng dạng.docx bằng phương pháp click vô nút Tải về tiếp sau đây.













Bình luận