1. TỌA ĐỘ CỦA MỘT VECTO 2. BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTO
1. TỌA ĐỘ CỦA MỘT VECTO
+) Trên mặt mày bằng, hệ trục bao gồm nhị trục Ox, Oy vuông góc cùng nhau bên trên O được gọi là hệ trục tọa độ.
Bạn đang xem: trong mặt phẳng tọa độ oxy
Quảng cáo
Mặt bằng chứa chấp hệ trục tọa phỏng Oxy gọi là mặt mày bằng tọa phỏng Oxy hoặc mặt bằng Oxy.
+) Vecto đơn vị là vecto phía là chiều dương, có tính nhiều năm bởi vì 1.
Quy ước: vecto đơn vị chức năng của trục Ox là \(\overrightarrow i \), vecto đơn vị chức năng của trục Oy là \(\overrightarrow j \).
Điểm O gọi là gốc tọa độ, trục Ox gọi là trục hoành, trục Oy gọi là trục tung.
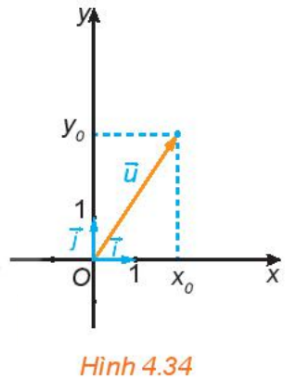
+) Với từng vecto \(\overrightarrow u \) bên trên mặt mày bằng Oxy, với độc nhất cặp số \(({x_0};{y_0})\) sao mang đến \(\overrightarrow u = {x_0}.\overrightarrow i + {y_0}.\overrightarrow j \)
Ta trình bày vecto \(\overrightarrow u \) với tọa phỏng \(({x_0};{y_0})\) và viết lách \(\overrightarrow u = ({x_0};{y_0})\) hoặc \(\overrightarrow u ({x_0};{y_0})\).
Các số \({x_0},{y_0}\) ứng được gọi là hoành phỏng, tung phỏng của \(\overrightarrow u \).
+) Hai vecto bởi vì nhau Lúc và chỉ Lúc bọn chúng với nằm trong tọa độ
\(\overrightarrow u (x;y) = \overrightarrow v (x';y') \Leftrightarrow \left\{ \begin{array}{l}x = x'\\y = y'\end{array} \right.\)
2. BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTO
+) Cho nhị vecto \(\overrightarrow u = (x;y)\) và \(\overrightarrow v = (x';y')\). Khi đó:
\(\begin{array}{l}\overrightarrow u + \overrightarrow v = (x + x';y + y')\\\overrightarrow u - \overrightarrow v = (x - x';y - y')\\k\overrightarrow u = (kx;ky)\quad (k \in \mathbb{R})\end{array}\)
+) Vecto \(\overrightarrow v \;(x';y')\) nằm trong phương với vecto \(\overrightarrow u \;(x;y) \ne \overrightarrow 0 \)
\( \Leftrightarrow \exists \;k \in \mathbb{R}:x' = kx,\;y' = ky\) hoặc \(\frac{{x'}}{x} = \frac{{y'}}{y}\) nếu như \(xy \ne 0.\)
Xem thêm: các chất điện li yếu
+) Điểm M với tọa phỏng \((x;y)\) thì vecto \(\overrightarrow {OM} \) với tọa phỏng \((x;y)\) và phỏng nhiều năm \(\left| {\overrightarrow {OM} } \right| = \sqrt {{x^2} + {y^2}} \)
+) Với nhị điểm \(M(x;y)\) và \(N(x';y')\) thì \(\overrightarrow {MN} = (x' - x;y' - y)\)
Khoảng cách thân mật nhị điểm M, N là \(MN = \left| {\overrightarrow {MN} } \right| = \sqrt {{{(x' - x)}^2} + {{(y' - y)}^2}} \)
+) Trung điểm M của đoạn trực tiếp AB với tọa phỏng là \(\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
+) Trọng tâm G của tam giác ABC với tọa phỏng là \(\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)

![]() Chia sẻ
Chia sẻ
-
Giải thắc mắc mở màn trang 59 SGK Toán 10 luyện 1 – Kết nối học thức
Một bạn dạng tin tưởng dự đoán không khí thể hiện tại lối đi nhập 12 giờ của một cơn sốt bên trên một phía bằng tọa phỏng. Trong khoảng tầm thời hạn cơ, tâm bāo dịch chuyển trực tiếp đều từ vựng trí với tọa phỏng (13,8; 108,3) cho tới địa điểm với toạ phỏng (14,1;106,3).
-
Giải mục 1 trang 60, 61 SGK Toán 10 luyện 1 - Kết nối học thức
Trên trục số Ox, gọi A là vấn đề màn trình diễn số 1 và đặt điều OA=i (H.4.32a). Gọi M là vấn đề màn trình diễn số 4, N là vấn đề màn trình diễn số -3/2. Hãy biểu thị từng vectơ OM, ON bám theo vectơ i Trong Hình 4.33: a) Hãy biểu thị từng vectơ OM, ON bám theo những vectơ i, j. Tìm tọa phỏng của vecto 0
-
Giải mục 2 trang 61, 62, 63, 64 SGK Toán 10 luyện 1 - Kết nối học thức
Trong mặt mày bằng tọa phỏng Oxy, mang đến u = (2; - 3), v = (4;1), a = (8; - 12 Trong mặt mày bằng tọa phỏng Oxy, mang đến điểm M(x0, y0). Gọi P.., Q ứng là hình chiếu vuông góc của M bên trên trục hoành Ox và trục tung Oy (H.4.35) Trong mặt mày bằng tọa phỏng Oxy, cho những điểm M(x;y) và N(x’; y’) Trong mặt mày bằng tọa phỏng Oxy, mang đến nhị điểm A(2; 1), B(3; 3). Từ vấn đề dự đoán được thể hiện ở đầu bài học kinh nghiệm, hãy xác lập tọa phỏng địa điểm M của tâm bão bên trên thời gian 9h trong vòng thời hạn 12 giờ của dự đoán.
-
Giải bài xích 4.16 trang 65 SGK Toán 10 luyện 1 – Kết nối học thức
Trong mặt mày bằng tọa phỏng Oxy, cho những điểm M(1; 3), N(4; 2) a) Tính phỏng nhiều năm những đoạn trực tiếp OM, ON, MN. b) Chứng minh rằng tam giác OMN vuông cân nặng.
-
Giải bài xích 4.17 trang 65 SGK Toán 10 luyện 1 – Kết nối học thức
Trong mặt mày bằng tọa phỏng Oxy, cho những vectơ a=3.i-2j , b={4; - 1} và những điểm M (-3; 6), N(3; -3). a) Tìm côn trùng tương tác trong số những vectơ MN và 2a-b. b) Các điểm O, M, N với trực tiếp mặt hàng hoặc không? c) Tìm điểm P(x; y) nhằm OMNP là 1 trong những hình bình hành.
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Kết nối học thức - Xem ngay
Xem thêm: cách đổi đơn vị đo khối lượng
2k8 Tham gia ngay lập tức group share, trao thay đổi tư liệu học hành miễn phí

>> Học trực tuyến Lớp 10 bên trên Tuyensinh247.com, Cam kết canh ty học viên học tập chất lượng, trả trả tiền học phí nếu như học tập ko hiệu suất cao.












Bình luận