Tính hóa học đàng khoảng của tam giác - Tìm hiểu tuyệt kỹ đo lường và tính toán hiệu quả
Chủ đề Tính hóa học đàng khoảng của tam giác: tạo nên những vấn đề cần thiết và hữu ích về đặc thù của đàng khoảng của tam giác. Đường khoảng của tam giác là đoạn trực tiếp nối nhì trung điểm ngẫu nhiên nhập tam giác, hùn phân chia tỷ trọng đoạn trực tiếp theo dõi một cơ hội đồng đều. Tính hóa học này hỗ trợ chúng ta nắm rõ rộng lớn về cấu hình và tỷ trọng của tam giác, thêm phần nhập việc giải quyết và xử lý những vấn đề tương quan cho tới tam giác một cơ hội đơn giản và dễ dàng và nhanh gọn.
Bạn đang xem: tính chất đường trung bình
Tính hóa học đàng khoảng của tam giác là đường thẳng liền mạch nối nhì trung điểm ngẫu nhiên nhập tam giác. Để tính chừng nhiều năm đàng khoảng của tam giác, tao dùng tấp tểnh lý Đường khoảng của tam giác.
- Định lý Đường khoảng của tam giác: Đường khoảng của tam giác là đoạn trực tiếp nối nhì trung điểm ngẫu nhiên nhập tam giác. Vậy nhập tam giác ABC, nếu như M là trung điểm của cạnh AB và N là trung điểm của cạnh BC, thì đường thẳng liền mạch MN là đàng khoảng của tam giác ABC.
- Độ nhiều năm đàng khoảng của tam giác: Độ nhiều năm đàng khoảng của tam giác bởi vì 50% chừng nhiều năm cạnh nhưng mà đàng khoảng tê liệt trải qua. Vì vậy, nhập tam giác ABC, nếu như MN là đàng khoảng thì chừng nhiều năm của đàng khoảng MN bởi vì 50% chừng nhiều năm cạnh AB.
Ví dụ: Cho tam giác ABC với cạnh AB có tính nhiều năm 10 centimet. Ta dò la trung điểm M của cạnh AB, và trung điểm N của cạnh BC. Sau tê liệt, tính chừng nhiều năm đàng khoảng MN.
- Trung điểm M: Để dò la trung điểm M của cạnh AB, tao phân chia chừng nhiều năm cạnh AB mang đến 2. Trong tình huống này, cạnh AB có tính nhiều năm 10 centimet, chính vì vậy chừng nhiều năm trung điểm M là 10 centimet / 2 = 5 centimet.
- Trung điểm N: Để dò la trung điểm N của cạnh BC, tao cũng phân chia chừng nhiều năm cạnh BC mang đến 2. Vì tất cả chúng ta ko biết chừng nhiều năm cạnh BC nhập ví dụ này, nên tao ko thể tính được chừng nhiều năm trung điểm N.
- Đường khoảng MN: Vì tao ko hiểu rằng chừng nhiều năm trung điểm N, nên ko thể tính được chừng nhiều năm đàng khoảng MN nhập ví dụ này.
Tóm lại, tính chất đường trung bình của tam giác là đường thẳng liền mạch nối nhì trung điểm ngẫu nhiên nhập tam giác. Độ nhiều năm của đàng khoảng bởi vì 50% chừng nhiều năm cạnh nhưng mà nó trải qua.
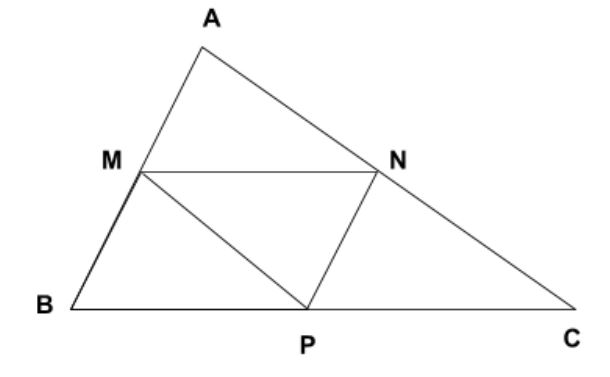
Đường khoảng của tam giác được khái niệm ra sao nhập toán học?
Trong toán học tập, đàng khoảng của tam giác được khái niệm là đoạn trực tiếp nối nhì trung điểm ngẫu nhiên nhập một tam giác. Ba cạnh của tam giác sẽ khởi tạo rời khỏi phụ thân đàng khoảng.
Cách tính đàng khoảng của tam giác như sau:
1. Gọi tam giác sở hữu phụ thân đỉnh là A, B, C và phụ thân cạnh ứng là a, b, c.
2. Đặt điểm trung điểm của cạnh AB là D, của cạnh BC là E và của cạnh AC là F.
3. Đường khoảng của tam giác AB là đoạn trực tiếp DE, của tam giác BC là đoạn trực tiếp EF và của tam giác AC là đoạn trực tiếp DF.
4. Để tính chừng nhiều năm đàng khoảng AB, tao cần thiết tính trung điểm của cạnh AB theo dõi công thức:
D = [(xA + xB)/2, (yA + yB)/2], nhập tê liệt (xA, yA) và (xB, yB) là tọa chừng của nhì đỉnh A và B.
5. Sau Khi sở hữu điểm trung điểm D, tao tính chừng nhiều năm đàng khoảng AB theo dõi công thức:
AB = sqrt((xD - xA)^2 + (yD - yA)^2).
6. Tương tự động, tao tính chừng nhiều năm những đàng khoảng còn sót lại EF và DF bởi vì những công thức tương tự động.
Ví dụ: Cho tam giác sở hữu phụ thân đỉnh là A(0, 0), B(4, 0) và C(2, 6). Để tính đàng khoảng AB, tao có:
- Trung điểm D của cạnh AB sở hữu tọa chừng là [(0 + 4)/2, (0 + 0)/2] = (2, 0).
- Độ nhiều năm của đàng khoảng AB là AB = sqrt((2 - 0)^2 + (0 - 0)^2) = sqrt(4) = 2.
Tương tự động, tao rất có thể tính chừng nhiều năm đàng khoảng EF và DF của tam giác theo dõi những công thức tương tự động nêu bên trên.
Tam giác sở hữu từng nào đàng trung bình?
Tam giác sở hữu 3 đàng khoảng. Mỗi đàng khoảng là đoạn trực tiếp nối trung điểm nhì cạnh của tam giác. Đường khoảng loại nhất nối trung điểm của cạnh loại nhất và cạnh loại nhì, đàng khoảng loại nhì nối trung điểm của cạnh loại nhì và cạnh loại phụ thân, và đàng khoảng loại phụ thân nối trung điểm của cạnh loại nhất và cạnh loại phụ thân. Vì vậy, tam giác sở hữu 3 đàng khoảng.

ĐỊNH NGHĨA, ĐỊNH LÍ, TÍNH CHẤT ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC. TOÁN LỚP 8 - P1
Đường khoảng tam giác: Quý Khách ham muốn dò la hiểu về đàng khoảng tam giác và cơ hội nó rất có thể khiến cho bạn giải quyết và xử lý những vấn đề hình học? Hãy coi Clip này nhằm nắm rõ rộng lớn về đàng khoảng tam giác và những phần mềm thú vị của chính nó nhập thực tiễn.
Cạnh nào là của tam giác đưa đến đàng khoảng ở tuy nhiên song với đàng khoảng đó?
Trong tam giác, đàng khoảng được khái niệm là đoạn trực tiếp nối nhì trung điểm ngẫu nhiên nhập tam giác. Để xác lập cạnh nào là của tam giác đưa đến đàng khoảng ở tuy nhiên song với đàng khoảng tê liệt, tất cả chúng ta rất có thể dùng quy tắc sau:
1. Xác tấp tểnh nhì trung điểm nhập tam giác: Trước tiên, tất cả chúng ta cần thiết xác lập nhì trung điểm ngẫu nhiên nhập tam giác. Trung điểm của một cạnh là vấn đề nằm tại thân thiết đoạn trực tiếp tê liệt.
2. Vẽ đàng trung bình: Sau Khi tiếp tục xác lập nhì trung điểm, tất cả chúng ta vẽ đường thẳng liền mạch nối nhì trung điểm tê liệt. Đường trực tiếp này được gọi là đàng khoảng của tam giác.
3. Xác tấp tểnh cạnh tương ứng: Để đàng khoảng của tam giác ở tuy nhiên song với cùng 1 cạnh rõ ràng, tao cần thiết đánh giá coi đàng khoảng hạn chế cạnh tê liệt hay là không. Nếu đàng khoảng hạn chế cạnh tê liệt, thì cạnh ứng ko đưa đến đàng khoảng tuy nhiên tuy nhiên. trái lại, nếu như đàng khoảng ko hạn chế cạnh tê liệt, thì cạnh tê liệt đưa đến đàng khoảng tuy nhiên tuy nhiên.
Ví dụ: Cho tam giác ABC, trung điểm của đoạn AB là D và trung điểm của đoạn AC là E. Vẽ đàng khoảng DE. Để xác lập cạnh của tam giác đưa đến đàng khoảng DE ở tuy nhiên song với đàng khoảng tê liệt, tất cả chúng ta đánh giá coi đàng khoảng DE sở hữu hạn chế cạnh BC hay là không. Nếu đàng DE ko hạn chế cạnh BC, tức là DE và BC tuy nhiên song cùng nhau.
Tuy nhiên, việc xác lập cạnh nào là của tam giác đưa đến đàng khoảng ở tuy nhiên song với đàng khoảng tê liệt cần thiết dựa vào những vấn đề rõ ràng về tam giác rõ ràng.
Độ nhiều năm đàng khoảng của tam giác tính như vậy nào?
Độ nhiều năm đàng khoảng của tam giác được xem như sau:
Bước 1: Xác tấp tểnh trung điểm của nhì cạnh của tam giác. Gọi A, B, C là phụ thân đỉnh của tam giác, và M, N, Phường là trung điểm của những cạnh ứng AB, BC, CA.
Bước 2: Tính chừng nhiều năm từng cạnh của tam giác. Gọi a, b và c là chừng nhiều năm phụ thân cạnh của tam giác. Sử dụng công thức khoảng cách thân thiết nhì điểm bên trên mặt mũi bằng hai phía, tao rất có thể tính được chừng nhiều năm những cạnh của tam giác.
Bước 3: Tính chừng nhiều năm đàng khoảng. Đường khoảng của tam giác là đoạn trực tiếp nối nhì trung điểm ngẫu nhiên nhập tam giác. Do tê liệt, tao chỉ việc tính chừng nhiều năm đoạn trực tiếp nối nhì trung điểm ngẫu nhiên.
Bước 4: kề dụng công thức tính khoảng cách thân thiết nhì điểm bên trên mặt mũi bằng hai phía, tao rất có thể tính được chừng nhiều năm đàng khoảng. Độ nhiều năm đàng khoảng của tam giác là bởi vì chừng nhiều năm đoạn trực tiếp nối nhì trung điểm ngẫu nhiên.
Ví dụ, nếu như tao xác lập trung điểm của cạnh AB và BC, và tính được chừng nhiều năm AB và BC, tao rất có thể tính chừng nhiều năm đàng khoảng của tam giác AMB.
Xem thêm: phân tích bài thơ mẹ và quả
_HOOK_
Đường khoảng của tam giác, của hình thang - Bài 4 - Toán 8 - Cô Huệ Chi (DỄ HIỂU NHẤT)
Đường khoảng hình thang: Quý Khách ham muốn nắm rõ định nghĩa về đàng khoảng hình thang và cơ hội nó vận dụng nhập giải những vấn đề hình học tập phức tạp? Xem Clip này nhằm chính thức cuộc hành trình dài mày mò vẻ rất đẹp và tính phần mềm của đàng khoảng hình thang.
Định nghĩa của trung điểm nhập tam giác là gì?
Định nghĩa của trung điểm nhập tam giác là vấn đề phía trên đoạn trực tiếp nối nhì đỉnh của tam giác và phân chia đoạn trực tiếp tê liệt trở thành nhì phần đều bằng nhau. Nghĩa là, cả nhì đoạn từ 1 đỉnh cho tới trung điểm và kể từ trung điểm cho tới đỉnh còn sót lại sở hữu nằm trong chừng nhiều năm. Trong tam giác, tao sở hữu phụ thân trung điểm ứng với phụ thân cạnh.
Đường khoảng của tam giác sở hữu mối quan hệ gì với trung điểm của cạnh?
Đường khoảng của tam giác sở hữu một mối quan hệ cần thiết với trung điểm của cạnh. Cụ thể, đàng khoảng của tam giác là đoạn trực tiếp nối nhì trung điểm ngẫu nhiên nhập tam giác tê liệt. Nếu tao ký hiệu tam giác ABC và M là trung điểm của cạnh AB, N là trung điểm của cạnh AC, thì đàng khoảng của tam giác ABC là đoạn trực tiếp MN.
Quan trọng rộng lớn, đương khoảng của tam giác là một trong đường thẳng liền mạch tuy nhiên song với cạnh loại phụ thân và có tính nhiều năm bởi vì nửa chừng nhiều năm của cạnh tê liệt. Vấn đề này Tức là MN tuy nhiên song với BC và có tính nhiều năm bởi vì 50% chừng nhiều năm của BC.
Đường khoảng của tam giác là một trong định nghĩa cần thiết nhập toán học tập và có rất nhiều phần mềm nhập lý thuyết tam giác và những vấn đề tương quan.
Cách đo lường và tính toán đàng khoảng nhập tam giác?
Cách tính đàng khoảng nhập tam giác như sau:
Bước 1: Xác tấp tểnh những trung điểm của nhì cạnh nhập tam giác. Gọi nhì cạnh này là AB và AC.
Bước 2: Tìm điểm trung điểm D của cạnh BC. Điểm D là uỷ thác điểm của đoạn trực tiếp AB và đoạn trực tiếp AC.
Bước 3: Vẽ đoạn trực tiếp CD. Đây đó là đàng khoảng của tam giác ABC.
Bước 4: Kiểm tra coi đàng khoảng CD sở hữu đưa đến phụ thân đoạn trực tiếp tuy nhiên song với những cạnh như nhập khái niệm ko. Nếu chính, việc làm đo lường và tính toán tiếp tục hoàn thành xong.
Cách tính đàng khoảng này dựa vào khái niệm của đàng khoảng nhập toán học tập.
Toán học tập lớp 8 - Bài 4 - Đường khoảng của tam giác và của hình thang
Toán học tập lớp 8: Quý Khách đang được học tập lớp 8 và ham muốn tóm Chắn chắn kiến thức và kỹ năng về toán học? Hãy coi Clip này nhằm dò la hiểu những định nghĩa, công thức và cách thức giải toán toán học tập lớp 8 một cơ hội trực quan liêu và thú vị. Hãy chính thức hành trình dài phát triển thành một bậc thầy toán học tập kể từ ngay lập tức giờ đây.
Tính hóa học cần thiết nào là của đàng khoảng được dùng trong những vấn đề tam giác?
Trong những vấn đề tam giác, đàng khoảng của tam giác sở hữu một vài đặc thù cần thiết được sử dụng:
1. Đường khoảng của tam giác luôn luôn trải qua trung điểm của cạnh ứng và nối trung điểm tê liệt với đỉnh ứng của tam giác. Vì vậy, nếu như sở hữu vấn đề về những trung điểm nhập tam giác, tao rất có thể dùng đàng khoảng nhằm tương tác trong số những trung điểm, những cạnh và những đỉnh của tam giác.
2. Một đàng khoảng của tam giác tuy nhiên song với cạnh loại phụ thân và có tính nhiều năm bởi vì 50% chừng nhiều năm cạnh tê liệt. Vấn đề này rất có thể được dùng nhằm dò la chừng nhiều năm đàng khoảng của tam giác lúc biết chừng nhiều năm những cạnh.
3. Đường khoảng của tam giác tạo nên trở thành những đoạn trực tiếp sở hữu những trung điểm không giống nhau và bọn chúng tỷ trọng cùng nhau theo dõi tỉ lệ thành phần 2:1. Vấn đề này rất có thể được dùng nhằm dò la những tỉ lệ thành phần thân thiết chừng nhiều năm những đoạn trực tiếp nhập tam giác.
4. Đường khoảng của tam giác uỷ thác nhau bên trên một điểm có một không hai, là trọng tâm của tam giác. Trọng tâm là vấn đề khoảng của những đỉnh tam giác và nó phân chia đàng khoảng trở thành phụ thân đoạn trực tiếp có tính nhiều năm đều bằng nhau. Qua tê liệt, tao rất có thể dùng đàng khoảng nhằm dò la trọng tâm của tam giác.
Tóm lại, đàng khoảng của tam giác có rất nhiều đặc thù cần thiết được dùng trong những vấn đề tam giác như tương tác trong số những trung điểm, dò la chừng nhiều năm và tỉ lệ thành phần của những đoạn trực tiếp, tương đương dò la trọng tâm của tam giác.
Xem thêm: phân tích người lái đò sông đà trữ tình
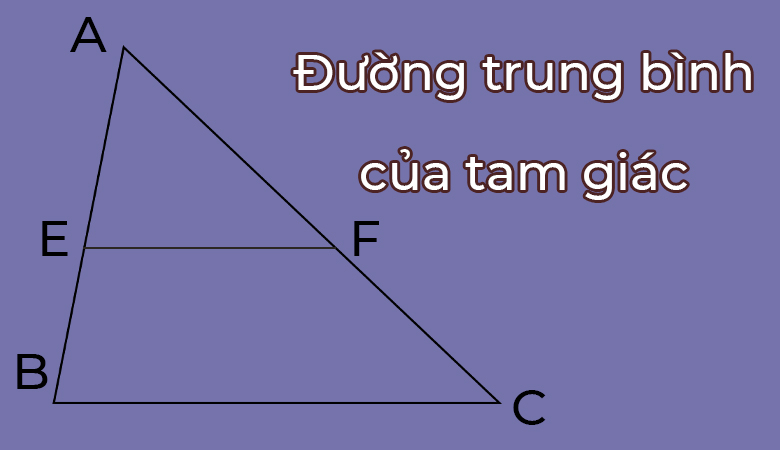
Trong tam giác, sở hữu quan hệ gì thân thiết đàng khoảng và đàng chéo?
Trong tam giác, đàng khoảng và đàng chéo cánh không tồn tại quan hệ thẳng cùng nhau. Mỗi tam giác sở hữu phụ thân đàng khoảng, là những đoạn trực tiếp nối từ 1 đỉnh của tam giác cho tới trung điểm của cạnh đối lập. Trong Khi tê liệt, từng tam giác cũng đều có phụ thân đàng chéo cánh, là những đoạn trực tiếp nối từ 1 đỉnh ko nên đỉnh của tam giác tới điểm uỷ thác của những đàng cao.
Tuy nhiên, nhập một vài tình huống đặc biệt quan trọng, tao rất có thể nhìn thấy quan hệ thân thiết đàng khoảng và đàng chéo cánh. Một tình huống nhất là tam giác vuông, Khi tê liệt đàng khoảng trải qua trung điểm của cạnh huyền và đàng chéo cánh là cạnh huyền của tam giác. Trong tình huống này, đàng khoảng và đàng chéo cánh là và một đoạn trực tiếp.
Tuy nhiên, nhập tình huống tam giác ko vuông, không tồn tại quan hệ thẳng thân thiết đàng khoảng và đàng chéo cánh. Chúng là nhì định nghĩa riêng lẻ và ko tương tự nhập tam giác.
_HOOK_











Bình luận