tâm của đường tròn ngoại tiếp tam giác

Đường tròn trĩnh nước ngoài tiếp tam giác là tổ hợp những kiến thức và kỹ năng kể từ định nghĩa, đặc điểm, những kiến thức và kỹ năng tương quan và những dạng bài bác tập dượt. Giúp chúng ta học viên hoàn toàn có thể hiểu thiệt rõ ràng về lối tròn trĩnh nước ngoài tiếp của tam giác, kể từ cơ nắm rõ những kiến thức và kỹ năng và giải đước toàn bộ những việc về lối tròn trĩnh nước ngoài tiếp những tam giác.

Bạn đang xem: tâm của đường tròn ngoại tiếp tam giác

1. Định nghĩa lối tròn trĩnh nước ngoài tiếp tam giác

Đường tròn trĩnh nước ngoài tiếp của một tam giác được hiểu là lối tròn trĩnh xúc tiếp phía ngoài của tam giác. Vậy nên tao đem tấp tểnh nghĩa: Đường tròn trĩnh nước ngoài tiếp tam giác là lối tròn trĩnh trải qua 3 đỉnh của một tam giác. Tâm của lối tròn trĩnh nước ngoài tiếp của tam giác được xác lập là gửi gắm điểm của 3 lối trung trực của tam giác cơ. Mé cạnh, cơ thì tất cả chúng ta còn tồn tại lối tròn trĩnh nội tiếp tam giác tiếp tục dò la hiểu tại đoạn sau nhé.

Đường tròn trĩnh nước ngoài tiếp tam giác còn hoàn toàn có thể được gọi với một chiếc thương hiệu không giống là tam giác nội tiếp lối tròn trĩnh (hay tam giác ở trong lối tròn).

Hình hình ảnh rõ ràng về lối tròn trĩnh nước ngoài tiếp của tam giác

Khi tổ chức nối tâm O của lối tròn trĩnh với 3 đỉnh của tam giác ABC thì sẽ sở hữu được những đường thẳng liền mạch : OA = OB = OC. Đó đó là nửa đường kính của đường tròn trĩnh nước ngoài tiếp tam giác ABC tuy nhiên tất cả chúng ta cần thiết dò la. Với công thức này, chúng ta học viên hoàn toàn có thể vận dụng nhằm giải quyết và xử lý không ít những dạng bài bác tương quan cho tới lối tròn trĩnh nước ngoài tiếp của tam giác.

2. Tính hóa học của lối tròn trĩnh nước ngoài tiếp tam giác

Với đường tròn trĩnh nước ngoài tiếp tam giác sẽ sở hữu những đặc điểm vô cùng cần thiết tuy nhiên chúng ta học viên cần thiết cầm thiệt kỹ sau đây:

• Một tam giác thì có duy nhất một và có một không hai một lối tròn trĩnh nước ngoài tiếp.
• Giao điểm của tía lối trung trực của một tam giác bất kì đó là tâm của đường tròn trĩnh nước ngoài tiếp tam giác đó.
• Đối với tam giác vuông thì trung điểm của cạnh huyền tam giác cơ đó là tâm của lối tròn trĩnh nước ngoài tiếp của tam giác.
• Với một tam giác đều thì tâm lối tròn trĩnh nước ngoài tiếp và nội tiếp của tam giác này sẽ nằm trong là 1 trong những điểm.

3. Một số kiến thức và kỹ năng không giống về lối tròn trĩnh nước ngoài tiếp tam giác

Bên cạnh những kiến thức và kỹ năng cơ bạn dạng về đường tròn trĩnh nước ngoài tiếp tam giác. Thì chúng ta học viên cũng cần phải chuẩn bị thêm vào cho bạn dạng thân thuộc một vài kiến thức và kỹ năng lý thuyết nâng lên về lối tròn trĩnh nước ngoài tiếp của tam giác nhằm hoàn toàn có thể đoạt được được thiệt nhiều những dạng toán tương quan.

3.1 Cách nhằm hoàn toàn có thể vẽ lối tròn trĩnh nước ngoài tiếp tam giác

Để hoàn toàn có thể xác lập thiệt đúng mực tâm của đường tròn trĩnh nước ngoài tiếp tam giác thì chúng ta học viên lưu ý thiệt kỹ kiến thức và kỹ năng sau đây: “ Tâm của lối tròn trĩnh nước ngoài tiếp với ngẫu nhiên một tam giác này luôn luôn là gửi gắm điểm của 3 lối trung trực tam giác đó”. 

Vậy nên lúc mong muốn vẽ lối tròn trĩnh nước ngoài tiếp của tam giác ABC thì thứ nhất tất cả chúng ta cần thiết vẽ tam giác, tiếp cơ kẻ những lối trung trực khởi nguồn từ 3 đỉnh của tam giác cơ nhằm hoàn toàn có thể xác lập tâm I của lối tròn trĩnh. Cuối nằm trong chỉ việc lấy nửa đường kính R= IA= IB= IC. Vậy là tất cả chúng ta hoàn toàn có thể vẽ được lối tròn trĩnh nước ngoài tiếp tam giác rồi cơ. 

3.2 Cách nhằm hoàn toàn có thể xác lập tâm lối tròn trĩnh nước ngoài tiếp tam giác

Để hoàn toàn có thể xác lập tâm của lối tròn trĩnh nước ngoài tiếp ngẫu nhiên tam giác này thì tất cả chúng ta đều cần thiết xác xác định trí gửi gắm điểm 3 lối trung trực của tam giác cơ. Hình như,thì tâm của lối tròn trĩnh nước ngoài tiếp của một tam giác cũng hoàn toàn có thể là gửi gắm của hai tuyến phố trung trực. Vậy nên đem nhị phương pháp để những chúng ta cũng có thể giải quyết và xử lý những việc dạng này thiệt dễ dàng và đơn giản.

Cách 1: Ta gọi I (x;y) là tâm của đường tròn trĩnh nước ngoài tiếp tam giác ABC tuy nhiên tất cả chúng ta cần thiết dò la. Theo đặc điểm của lối tròn trĩnh nước ngoài tiếp tao sẽ sở hữu IA = IB = IC = R. Lúc này toạ chừng xác lập của tâm I (x;y) được xem là nghiệm của phương trình:

IA^2 = IB^2

IA^2 = IC^2

Cách 2: Với sử dụng phương pháp này tất cả chúng ta tiếp tục cần thiết áp dụng kiến thức và kỹ năng nhằm ghi chép phương trình hai tuyến phố trung trực của nhị cạnh nằm trong tam giác. Tiếp cơ, cần thiết xác lập gửi gắm điểm của hai tuyến phố trung trực cơ dựa vào những kiến thức và kỹ năng tuy nhiên tất cả chúng ta đang được học tập. Tâm của đường tròn trĩnh nước ngoài tiếp tam giác đó là gửi gắm điểm của hai tuyến phố trung trực này.

Xem thêm: công thức quá khứ hoàn thành

Lưu ý: Với tam giác vuông thì tâm của đường tròn trĩnh nước ngoài tiếp tam giác này đó là trung điểm của cạnh huyền. Cạnh huyền cũng đó là 2 lần bán kính của lối tròn trĩnh nước ngoài tiếp của tam giác cơ.

3.2 Phương trình cụ thể của lối tròn trĩnh nước ngoài tiếp tam giác

Một số dạng toán nâng lên tiếp tục đòi hỏi chúng ta học viên nên ghi chép được phương trình của đường tròn trĩnh nước ngoài tiếp tam giác. Vừa mới nhất nghe qua quýt thì hoàn toàn có thể những học viên tiếp tục thấy đó là một dạng bài bác khá khó khăn. Tuy nhiên, chỉ việc nắm rõ quá trình tại đây thì việc giải  việc này sẽ rất dễ dàng dàng:

• Bước 1: Cần gán tọa chừng những đỉnh của tam giác nội tiếp lối tròn trĩnh nhập phương trình đem ẩn a,b,c. Do khoảng cách kể từ tâm lối tròn trĩnh cho tới những đỉnh đó là nửa đường kính nên những đỉnh nằm trong hoặc phía trên lối tròn trĩnh nước ngoài tiếp. Vì thế tuy nhiên tọa chừng của những đỉnh tiếp tục thoả mãn phương trình tuy nhiên tất cả chúng ta cần thiết dò la.
• Bước 2: Tiến hành giải hệ phương trình tiếp tục triển khai thay cho thế những đỉnh phía trên nhằm dò la đi ra những thành phẩm a,b,c
• Bước 3: Do A, B và C nằm trong lối tròn trĩnh nên tao đem hệ phương trình:

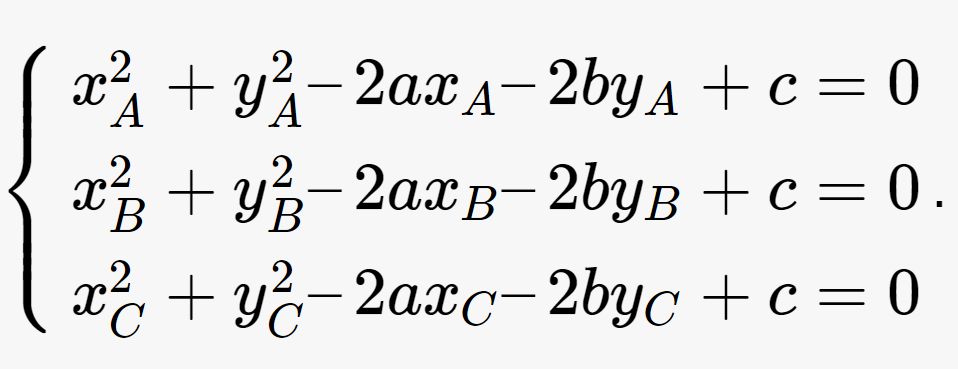
=> Sau Khi giải hệ phương trình bên trên tao tiếp tục xác lập được a, b, c.

3.3 Cách tính nửa đường kính lối tròn trĩnh nước ngoài tiếp tam giác chuẩn chỉnh nhất

Đây là dạng bài bác khá thông thường bắt gặp trong số kỳ đua đánh giá kế hoạch. Do cơ, chúng ta học viên cần thiết nắm vững và cụ thể thủ tục tại đây nhằm triển khai xong bài bác đua một cơ hội cực tốt. 

Ví dụ: Với đề bài bác mang đến tam giác ABC đem những cạnh là AB, AC và BC. Thay theo thứ tự những cạnh AB, AC và BC trở nên những ẩn a,b,c của phương trình. Ta tiếp tục tính được nửa đường kính nước ngoài tiếp của tam giác ABC theo dõi công thức sau:

Công thức cụ thể nhằm tính nửa đường kính của lối tròn trĩnh nước ngoài tiếp của tam giác

4. Một số bài bác tập dượt về lối tròn trĩnh nước ngoài tiếp tam giác

Dưới trên đây, công ty chúng tôi tiếp tục ra mắt cho tới chúng ta một vài việc về đường tròn trĩnh nước ngoài tiếp tam giác để chúng ta hiểu và triển khai xong những bài bác tập dượt một cơ hội cực tốt.

Bài 1: Viết phương trình lối tròn trĩnh nội tiếp của tam giác ABC Khi tiếp tục mang đến sẵn tọa chừng của 3 đỉnh A(-1;3); B(5;1); C(-2;3)

Bài 2: Cho tam giác ABC tiếp tục biết A(1;3), B(-1;1), C(2;2). Tìm tọa chừng của tâm lối tròn trĩnh nước ngoài tiếp của tam giác ABC.

Bài 3: Cho tam giác ABC đều với cạnh vày 8cm. Xác tấp tểnh nửa đường kính và tâm của lối tròn trĩnh nước ngoài tiếp của tam giác ABC?

Bài 4: Cho tam giác ABC đều với cạnh vày 10cm. Xác tấp tểnh nửa đường kính và tâm của lối tròn trĩnh nước ngoài tiếp của tam giác ABC?

Xem thêm: tứ giác đều là hình gì

Bài 5: Cho tam giác ABC vuông bên trên A, và AB=6 centimet, BC=8 centimet,. Xác tấp tểnh tâm và nửa đường kính đường tròn trĩnh nước ngoài tiếp tam giác ABC, Tính nửa đường kính lối tròn trĩnh nước ngoài tiếp của tam giác vày bao nhiêu?

Bài 6: Cho tam giác MNP đem tía góc nhọn nội tiếp nhập lối tròn trĩnh (O; R). Ba lối của tam giác là MF, NE và PD rời nhau bên trên H. Chứng minh tứ giác NDEP là tứ giác nội tiếp.

Trên trên đây, công ty chúng tôi đã hỗ trợ chúng ta học viên dành được tổ hợp những vấn đề cần phải biết về đường tròn trĩnh nước ngoài tiếp tam giác. Mong rằng với những vấn đề này sẽ hỗ trợ những học viên đem thêm vào cho bản thân hành trang hữu ích mang đến môn toán. Đừng quên theo dõi dõi công ty chúng tôi nhằm tìm hiểu thêm thắt thiệt nhiều những kiến thức và kỹ năng toán học tập hữu ích nhé.