Chủ đề hình tứ diện đều phải có từng nào mặt mũi đối xứng: Hình tứ diện đều phải có tổng số 6 mặt mũi đối xứng, tạo ra sự phẳng phiu và thích mắt của hình học tập. Mỗi mặt mũi phẳng phiu đối xứng có một cạnh và trung điểm của cạnh đối lập. Vấn đề này dẫn đến một sự đối xứng tuyệt đối Một trong những mặt mũi, tạo ra một hình hình họa hợp lý và tự động hóa hấp dẫn sự quan hoài của những người nhìn.
Hình tứ diện đều phải có từng nào mặt mũi đối xứng?
Hình tứ diện đều phải có 6 mặt mũi đối xứng. Mỗi mặt mũi phẳng phiu đối xứng được tạo nên vì thế một cạnh với trung điểm của cạnh đối lập của chính nó. Vấn đề này Tức là tứ diện đều phải có 6 mặt mũi phẳng phiu đối xứng, từng mặt mũi phẳng phiu chứa chấp 1 cạnh và trung điểm cạnh đối lập tạo nên trở nên tứ diện đều.
Bạn đang xem: khối tứ diện đều có bao nhiêu mặt phẳng đối xứng
Hình tứ diện đều là gì?
Hình tứ diện đều là một trong hình học tập không khí sở hữu 4 mặt mũi phẳng phiu đều và những cạnh có tính nhiều năm cân nhau. Mỗi mặt mũi phẳng phiu đều là một trong tam giác đều và gặp gỡ nhau bên trên những cạnh sẽ tạo trở nên 4 góc nhọn bên trên một điểm gọi là đỉnh của tứ diện đều.
Để nắm rõ rộng lớn về hình tứ diện đều, tớ hoàn toàn có thể vận dụng khái niệm và đặc thù của nó:
1. Mặt phẳng phiu đối xứng: Tứ diện đều phải có 6 mặt mũi phẳng phiu đối xứng. Mỗi mặt mũi phẳng phiu đều có một cạnh và trung điểm của cạnh đối lập.
2. Số cạnh: Tứ diện đều phải có tổng số 6 cạnh đều, nhập cơ từng cạnh đều kiểu như nhau về chừng nhiều năm.
3. Số đỉnh: Tứ diện đều phải có 4 đỉnh, từng đỉnh ở giao phó nhau của 3 mặt mũi phẳng phiu đều và ứng với 3 cạnh.
4. Một số đặc thù khác: Tứ diện đều phải có ổ đĩa nước ngoài tiếp sở hữu nửa đường kính vì thế nửa chừng nhiều năm một cạnh và hoàn toàn có thể được coi như là một trong tứ giác đều ở hình chiếu của chính nó bên trên mặt mũi phẳng phiu xy.
Với những đặc thù bên trên, hình tứ diện đều là một trong hình học tập giản dị và đơn giản tuy nhiên đặc biệt quan trọng về mặt mũi đối xứng và đều nhau.
Tứ diện đều phải có từng nào mặt mũi đối xứng?
Tứ diện đều phải có 6 mặt mũi đối xứng.
Một mặt mũi đối xứng được tạo nên vì thế một cạnh và trung điểm của cạnh đối lập của chính nó. Vấn đề này Tức là nếu như tất cả chúng ta liên kết một cạnh ngẫu nhiên của tứ diện đều với trung điểm của cạnh đối lập của chính nó, tất cả chúng ta sẽ khởi tạo đi ra một phía phẳng phiu đối xứng.
Tứ diện đều cũng hoàn toàn có thể được xem như là một hình học tập sắc lặc, tức thị từng mặt mũi đều phải có nằm trong số cạnh và nằm trong chừng nhiều năm những cạnh. Ví dụ, từng mặt mũi của tứ diện đều đều phải có tía cạnh và cạnh sở hữu nằm trong chừng nhiều năm.
Với sự đối xứng của những mặt mũi và cạnh, tứ diện đều trở nên một hình dễ thương và thích mắt.
Tìm mặt mũi phẳng phiu đối xứng của khối nhiều diện - Tính hóa học đối xứng của khối nhiều diện
\"Mặt phẳng phiu đối xứng là một trong định nghĩa thú vị nhập toán học tập, và video clip Shop chúng tôi share tiếp tục giúp cho bạn nắm rõ rộng lớn về nó. Hãy coi video clip ngay lập tức nhằm mày mò những đặc thù và phần mềm thú vị của mặt mũi phẳng phiu đối xứng!\"
Mỗi mặt mũi đối xứng của tứ diện đều phải có đặc thù gì?
Mỗi mặt mũi đối xứng của tứ diện đều phải có đặc thù như sau:
- Một mặt mũi phẳng phiu đối xứng là một trong mặt mũi phẳng phiu được dẫn đến vì thế một cạnh của tứ diện đều và trung điểm của cạnh đối lập với cạnh cơ.
- Tứ diện đều phải có tổng số 6 mặt mũi phẳng phiu đối xứng.
- Mỗi mặt mũi phẳng phiu đối xứng có một cạnh của tứ diện đều và trung điểm của cạnh đối lập.
- Mặt phẳng phiu đối xứng hạn chế tứ diện đều trở nên nhị nửa tứ diện cân nhau.
- Mặt phẳng phiu đối xứng thực hiện cho tới cấu tạo của tứ diện đều hành động tự nhiên qua quýt mặt mũi phẳng phiu cơ bám theo một loại đối xứng.
- Tính hóa học của mặt mũi đối xứng canh ty tứ diện đều phải có hình dạng đồng đều và thích mắt.
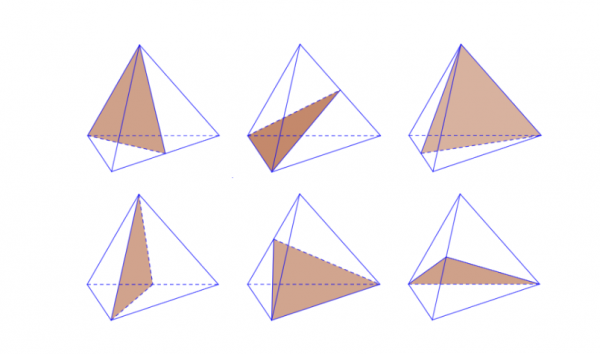
Cách tạo nên mặt mũi phẳng phiu đối xứng bên trên tứ diện đều như vậy nào?
Để tạo nên một phía phẳng phiu đối xứng bên trên một tứ diện đều, tất cả chúng ta hoàn toàn có thể tuân theo quá trình sau đây:
Bước 1: Vẽ một quãng trực tiếp nối nhị đỉnh ngẫu nhiên bên trên tứ diện đều. Đoạn trực tiếp này được xem là cạnh của mặt mũi phẳng phiu đối xứng tuy nhiên tất cả chúng ta mong muốn tạo nên.
Bước 2: Tìm trung điểm của đoạn trực tiếp đang được vẽ ở bước trước, cơ là vấn đề nằm tại vị trí thân ái đoạn trực tiếp cơ.
Bước 3: Vẽ một quãng trực tiếp nối trung điểm một vừa hai phải lần ở bước trước với đỉnh sót lại bên trên tứ diện đều. Đoạn trực tiếp này là đoạn vuông góc với đoạn trực tiếp ở bước 1 và trải qua trung điểm ở bước 2.
Bước 4: Các bước bên trên được tái diễn cho những cặp đỉnh không giống nhau bên trên tứ diện đều sẽ tạo đi ra những cạnh không giống của mặt mũi phẳng phiu đối xứng.
Bước 5: Cuối nằm trong, những đoạn trực tiếp một vừa hai phải vẽ ở quá trình bên trên sẽ khởi tạo trở nên mặt mũi phẳng phiu đối xứng tuy nhiên tất cả chúng ta đang được lần kiếm bên trên tứ diện đều.
Lưu ý rằng tứ diện đều phải có tổng số 6 mặt mũi phẳng phiu đối xứng, từng mặt mũi có một cạnh và trung điểm của cạnh đối lập.
_HOOK_
TOÁN 12 BÁT DIỆU VÀ MẶT PHẲNG ĐỐI XỨNG
\"Bát điệu không những là một trong trò đùa truyền thống cuội nguồn mà còn phải là một trong thẩm mỹ đậm màu dân gian lận. Video của Shop chúng tôi tiếp tục chỉ dẫn chúng ta cơ hội màn trình diễn chén điệu một cơ hội tinh tế và sắc sảo và tạo ra những điệu nhảy thú vị. Hãy coi ngay lập tức nhằm mày mò trái đất chén điệu!\"
Tại sao tứ diện đều phải có 6 mặt mũi đối xứng?
Tự diện là một trong nhiều diện sở hữu tứ diện lòng và toàn bộ những cạnh cân nhau. Một tứ diện đều phải có 6 mặt mũi đối xứng vì thế những cặp mặt mũi đối lập nhau trải qua những trục đối xứng. Dưới đó là lí vì thế vì sao tứ diện đều phải có 6 mặt mũi đối xứng:
1. Mỗi tứ diện đều phải có 3 trục đối xứng: Mỗi trục đối xứng trải qua trung điểm của một cạnh và đối lập với mặt mũi đối lập. Tứ diện đều phải có 4 cạnh, nên sở hữu tổng số 4x3 = 12 trục đối xứng. Tuy nhiên, vì thế từng trục đối xứng trải qua trung điểm của nhị cạnh, nên những trục đối xứng tạo nên trở nên 6 cặp trục đối xứng.
2. Mỗi cặp mặt mũi đối xứng qua quýt một trục đối xứng: Khi tất cả chúng ta cù tứ diện đều xung xung quanh một trục đối xứng, những mặt mũi được cù qua quýt bản thân chủ yếu. Mỗi trục đối xứng chứa chấp cạnh qua quýt trung điểm và đối lập mặt mũi, bởi vậy, dẫn đến một phía đối xứng.
Do cơ, tứ diện đều phải có tổng số 6 mặt mũi đối xứng.
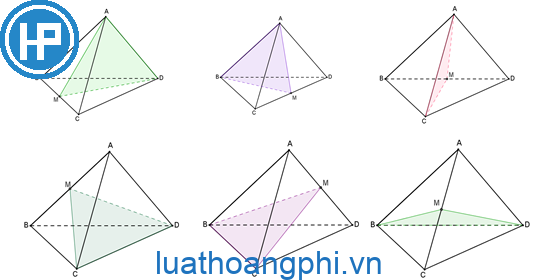
Mặt phẳng phiu đối xứng bên trên tứ diện đều được dẫn đến bằng phương pháp nào?
Một tứ diện đều phải có 6 mặt mũi phẳng phiu đối xứng. Mỗi mặt mũi phẳng phiu đối xứng được dẫn đến bằng phương pháp chứa chấp 1 cạnh của tứ diện và trung điểm của cạnh đối lập của chính nó. Vấn đề này Tức là nếu như tất cả chúng ta vẽ những đường thẳng liền mạch kể từ trung điểm của từng cạnh cho tới một điểm phân biệt phía trên cạnh đối lập, thì tất cả chúng ta sẽ khởi tạo đi ra một phía phẳng phiu đối xứng. Tổng nằm trong, tứ diện đều phải có 6 mặt mũi phẳng phiu đối xứng.
Đặc điểm công cộng của những mặt mũi đối xứng bên trên tứ diện đều là gì?
Đặc điểm công cộng của những mặt mũi đối xứng bên trên tứ diện đều là:
- Tứ diện đều phải có 6 mặt mũi phẳng phiu đối xứng.
- Mỗi mặt mũi phẳng phiu đối xứng có một cạnh của tứ diện và trung điểm cạnh đối lập.
- Các mặt mũi phẳng phiu đối xứng bên trên tứ diện đều phải có và một hình dạng và độ cao thấp.
- Chúng tạo nên trở nên hình dạng đối xứng xung xung quanh điểm tâm của tứ diện.
Video chỉ dẫn xác lập những mặt mũi phẳng phiu đối xứng của khối nhiều diện
\"Bạn đang được lần kiếm video clip chỉ dẫn về một yếu tố cụ thể? Không cần thiết lần kiếm thêm! Chúng tôi sở hữu video clip chỉ dẫn không thiếu về nhiều chủ thể thông dụng. Hãy coi ngay lập tức nhằm tích lũy những kỹ năng và khả năng mới!\"
Trên tứ diện đều, từng mặt mũi đối xứng chứa chấp những điểm nào?
Trên tứ diện đều, từng mặt mũi đối xứng chứa chấp nhị đỉnh và trung điểm của cạnh nối nhị đỉnh đối lập. Nói cách thứ hai, mặt mũi đối xứng của tứ diện đều chứa chấp chính tía điểm: nhị đỉnh và một trung điểm của cạnh đối lập.

Xem thêm: điểm chuẩn đại học thăng long 2022
Tứ diện đều được xác lập vì thế những Đặc điểm gì?
Tứ diện đều được xác lập vì thế những Đặc điểm sau:
1. Số mặt mũi phẳng phiu đối xứng: Tứ diện đều phải có 6 mặt mũi phẳng phiu đối xứng. Mỗi mặt mũi phẳng phiu đối xứng có một cạnh và trung điểm của cạnh đối lập.
2. Góc Một trong những mặt: Trên từng mặt mũi của tứ diện đều, sở hữu 3 cạnh gặp gỡ nhau bên trên những điểm gọi là đỉnh. Các đỉnh này tạo nên trở nên 4 góc cân nhau, từng góc đều là góc đối lập với cùng 1 cạnh.
3. Độ nhiều năm những cạnh: Tất cả những cạnh của tứ diện đều phải có chừng nhiều năm cân nhau.
4. Số đỉnh: Tứ diện đều phải có tổng số 4 đỉnh.
5. Dạng hình: Tứ diện đều phải có hình dạng học tập đều, tức thị những mặt mũi và cạnh đều nhau, mặt mũi kề nhau là đồng phẳng phiu và góc Một trong những mặt mũi cũng đều.
Tóm lại, tứ diện đều là một trong hình học tập đều bao gồm 4 mặt mũi phẳng phiu đều nhau, 6 mặt mũi đối xứng, 4 đỉnh và những cạnh có tính nhiều năm cân nhau.
_HOOK_
HH12 chương 1, buổi 1: Mặt phẳng phiu đối xứng, khối nhiều diện đều
\"HH12 chương một là 1 phần cần thiết nhập lịch trình học tập của bạn? Chúng tôi đang được dẫn đến một video clip rất tốt không thiếu những nội dung nhập chương này. Hãy coi ngay lập tức nhằm nắm rõ kỹ năng và sẵn sàng chất lượng cho tới bài xích đánh giá tiếp theo sau của bạn!\"










.jpg)


Bình luận