Tìm m nhằm hàm số không có cực trị (hàm số bậc 3) với điều giải nhằm chúng ta tìm hiểu thêm.
KHÓA ÔN CHUYÊN ĐỀ THI TỐT NGHIỆP THPT
Bạn đang xem: hàm số không có cực trị
NHANH CHÓNG LẤP LỖ HỔNG KIẾN THỨC - TỰ TIN NHẬP CUỘC ĐƯỜNG ĐUA ĐẠI HỌC
✅ Hệ thống hóa kỹ năng trọng tâm theo đòi từng mục chính đua đảm bảo chất lượng nghiệp THPT
✅ Cung cung cấp những cách thức thực hiện bài bác hiệu suất cao theo đòi từng thường xuyên đề THPT
✅ Lưu ý những lỗi sai thông thường gặp gỡ và tips, mẹo tăng thêm vận tốc thực hiện bài
✅ Đầy đầy đủ những môn Toán - Lí - Hóa - Anh - Văn - Sinh - Sử - Địa - GDCD
✅ Học phí chỉ 50K/chuyên đề

Tham khảo thêm:
- Cực trị của hàm số
- Tìm m nhằm hàm số với 7 rất rất trị
- Tìm m nhằm hàm số với 3 rất rất trị
Xét hàm số sau: nó = ax3 + bx2 + cx + d với a ≠ 0
Khi cơ y’ = 3ax2 + 2bx+c với y’ = 0 ⇔ 3ax2 + 2bx+c=0
Hàm số không tồn tại rất rất trị Lúc và chỉ Lúc phương trình y’ = 0 vô nghiệm hoặc là với nghiệm kép ⇔ Δ’ ≤ 0 ⇔ b2-3ac ≤ 0
Tìm m nhằm hàm số không có cực trị – Bài tập
Tìm m nhằm hàm số không có cực trị (ví dụ 1)
Tìm tổng số độ quý hiếm vẹn toàn của m nhằm hàm số
![]() không với rất rất trị:
không với rất rất trị:
- A. 5
- B. 3
- C. 4
- D. 7
Lời giải chi tiết
Đáp án đúng: A
Ta với y’ = x2 + 2mx – (2m – 3)
Xét y’ = 0 ⇔ x2 + 2mx – (2m – 3) = 0
Hàm số vẫn không tồn tại rất rất trị Lúc vài ba chỉ Lúc y’ = 0 với tối nhiều 1 nghiệm
Xem thêm: nhất chí hay nhất trí
⇔ Δ’ ≤ 0 ⇔ m2 + (2m – 3) ≤ 0 ⇔ -3 ≤m≤ 1
Kết phù hợp với ĐK m vẹn toàn nên m{-3;-2;-1;0;1}
Vậy sẽ sở hữu 5 độ quý hiếm m thỏa mãn nhu cầu đòi hỏi vấn đề.
Tìm m nhằm hàm số không có cực trị (ví dụ 2)
Với độ quý hiếm này của thông số m thì hàm số nó = x3 – 3x2 + 3(1 – m2)x + 1 tiếp tục không tồn tại rất rất trị.
- A. m ≠ 2
- B. m ∈ R
- C. m = 0
- D. Không tồn bên trên m
Lời giải chi tiết
Đáp án đúng: C
Ta với y’ = 3x2 – 6x + 3(1 – m2) với y’ = 0 ⇔ x2-2x + 1 – m2 = 0
Hàm số vẫn cho tới tiếp tục không tồn tại điểm rất rất trị Lúc phương trình y’ = 0 vô nghiệm hoặc với nghiệm kép ⇔ Δ’ ≤ 0 ⇔ 1 – (1 – m2) ≤ 0 ⇔ m2 ≤ 0 vậy m=0 thỏa mã đòi hỏi vấn đề.
Tìm m nhằm hàm số không có cực trị (ví dụ 3)
Cho hàm số sau: nó = -2x3+(2m – 1)x2-(m2 – 1)x – 2. Tìm toàn bộ những độ quý hiếm của thông số m nhằm hàm số vẫn cho tới tiếp tục không tồn tại rất rất trị .
Lời giải chi tiết
Chúng tớ với y’ = -6x2 + 2(2m – 1)x – (m2 – 1) với y’ = 0 ⇔ -6x2 + 2(2m – 1)x – (m2 – 1) = 0
Hàm số vẫn cho tới tiếp tục không tồn tại rất rất trị Lúc phương trình y’ = 0 với vô nghiệm hoặc là với nghiệm kép

Tìm m nhằm hàm số không có cực trị (ví dụ 4)
Tìm toàn bộ những độ quý hiếm của thông số m nhằm hàm số ![]() sẽ không tồn tại rất rất trị.
sẽ không tồn tại rất rất trị.
Lời giải chi tiết
– Với tình huống m=1 hàm số vẫn cho tới tiếp tục phát triển thành nó = 3x2 + x + 2 đó là hàm số bậc nhị nên luôn luôn chỉ mất có một không hai 1 rất rất trị.
→ Vậy với m=1 (loại)
– Trường thích hợp m ≠ 1, với y’ = (m – 1)x2 + 2(m + 2)x + m với y’ = 0 ⇔ (m – 1)x2 + 2(m + 2)x + m = 0
Xem thêm: vai trò của liên xô trong chiến tranh thế giới thứ 2
Hàm số vẫn cho tới tiếp tục không tồn tại rất rất trị Lúc phương trình y’ = 0 vô nghiệm hoặc là với nghiệm kép
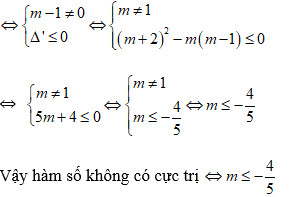
Trên đó là một trong những bài bác tập Tìm m nhằm hàm số không có cực trị với điều giải (toán 12) nhằm chúng ta tìm hiểu thêm.












Bình luận