Chủ đề mong muốn tính diện tích S hình tam giác đều: Quý Khách mong muốn tính diện tích S hình tam giác đều? Đó là 1 trong Việc thú vị! Hình tam giác đều sở hữu những cạnh đều bằng nhau, điều này đồng nghĩa tương quan với việc diện tích S cũng khá được tính theo gót công thức đơn giản và dễ dàng. Quý Khách chỉ việc nhân nhiều năm lối cao của tam giác với 1/2 chiều nhiều năm cạnh ngẫu nhiên là tiếp tục sở hữu sản phẩm. Hãy vừa lòng sự tò lần và đo lường và tính toán nhằm mày mò diện tích S của tam giác đều!
Làm sao nhằm tính diện tích S của một hình tam giác đều?
Để tính diện tích S của một hình tam giác đều, tất cả chúng ta rất có thể dùng công thức giản dị như sau:
1. Gọi a là chừng nhiều năm một cạnh của tam giác đều.
2. sát dụng công thức tính diện tích S tam giác: Diện tích = (cạnh x cạnh x căn bậc nhì của 3) / 4.
3. Thay vô công thức, tao có: Diện tích = (a x a x căn bậc nhì của 3) / 4.
4. Tính toán độ quý hiếm của căn bậc nhì của 3: căn bậc nhì của 3 ≈ 1.732.
5. Tiếp theo gót, tính diện tích S bằng phương pháp thay cho độ quý hiếm của căn bậc nhì của 3 vô công thức: Diện tích = (a x a x 1.732) / 4.
6. Rút gọn gàng công thức tao được: Diện tích = a^2 x 1.732 / 4.
7. Tiếp bại liệt, đo lường và tính toán diện tích S bằng phương pháp thay cho độ quý hiếm của a vô công thức: Diện tích = (a^2 x 1.732) / 4.
Với công việc bên trên, bạn cũng có thể đo lường và tính toán diện tích S của một hình tam giác đều đơn giản và dễ dàng.
Bạn đang xem: công thức tam giác đều

Tam giác đều là gì?
Tam giác đều hoặc còn được gọi là tam giác đồng đều là 1 trong loại tam giác quan trọng sở hữu những cạnh đều bằng nhau và những góc bên phía trong đều đạt độ quý hiếm 60 chừng. Vấn đề này Tức là chừng nhiều năm của cạnh a, cạnh b và cạnh c đều đều bằng nhau.
Để tính diện tích S của một tam giác đều, tao rất có thể dùng công thức A = (Cạnh x Cạnh x căn bậc nhì của ba) / 4.
Ví dụ, fake sử tam giác sở hữu cạnh có tính nhiều năm là 6 centimet. Ta thay cho độ quý hiếm vô công thức:
A = (6 x 6 x căn bậc nhì của 3) / 4
A = (36 x căn bậc nhì của 3) / 4
A ≈ 15.588 cm^2
Vậy diện tích S của tam giác đều sở hữu cạnh vị 6 centimet là khoảng chừng 15.588 cm^2.
Chúng tao cũng rất có thể tính diện tích S của tam giác đều bằng phương pháp dùng công thức hình tam giác, với chừng nhiều năm cạnh a là cạnh của tam giác đều.
A = (a^2 x căn bậc nhì của 3) / 4
Ở ví dụ bên trên, cạnh a = 6 centimet, vậy:
A = (6^2 x căn bậc nhì của 3) / 4
A = (36 x căn bậc nhì của 3) / 4
A ≈ 15.588 cm^2
Như vậy, tao cũng nhận được sản phẩm là khoảng chừng 15.588 cm^2.
Đây đó là phương pháp tính diện tích S tam giác đều và khái niệm của tam giác đều vô toán học tập.
Tại sao tam giác đều sở hữu 3 cạnh vị nhau?
Tam giác đều sở hữu 3 cạnh đều bằng nhau vì như thế đặc điểm quan trọng của những góc vô tam giác đều. Mỗi góc vô tam giác đều đều sở hữu độ quý hiếm là 60 chừng. Vấn đề này kéo theo những cạnh của tam giác đều sở hữu chừng nhiều năm đều bằng nhau.
Để nắm rõ rộng lớn về tại vì sao tam giác đều sở hữu 3 cạnh đều bằng nhau, tất cả chúng ta rất có thể cút thâm thúy vô đặc điểm của tam giác đều.
Tam giác đều sở hữu nhì đặc điểm quan liêu trọng:
1. Các cạnh của tam giác đều vị nhau: Vấn đề này đồng nghĩa tương quan với việc tía đoạn trực tiếp nối nhì đỉnh tiếp tục của tam giác đều sở hữu chừng nhiều năm đều bằng nhau.
2. Các góc vô tam giác đều đều sở hữu độ quý hiếm là 60 độ: Tất cả những góc vô tam giác đều đều sở hữu độ quý hiếm đều bằng nhau và đều vị 60 chừng.
Khi tao minh chứng đặc điểm loại nhất, tao dùng công thức Pythagoras nhằm tính lối chéo cánh của tam giác đều. Khi vận dụng công thức này, tao tiếp tục thấy rằng lối chéo cánh của tam giác đều sở hữu chừng nhiều năm vị với những cạnh của tam giác. Do bại liệt, những cạnh của tam giác đều đều bằng nhau.
Khi tao minh chứng đặc điểm loại nhì, tao dùng những công thức cơ phiên bản của hình học tập tam giác. phẳng phiu cơ hội minh chứng những góc của tam giác đều đều bằng nhau, tao rất có thể dùng những công thức góc tam giác nhằm minh chứng rằng toàn bộ những góc vô tam giác đều sở hữu độ quý hiếm là 60 chừng.
Tóm lại, tam giác đều sở hữu 3 cạnh đều bằng nhau vì như thế đặc điểm của những góc vô tam giác đều. Tính hóa học này quan trọng và phân biệt tam giác đều với những dạng tam giác không giống.
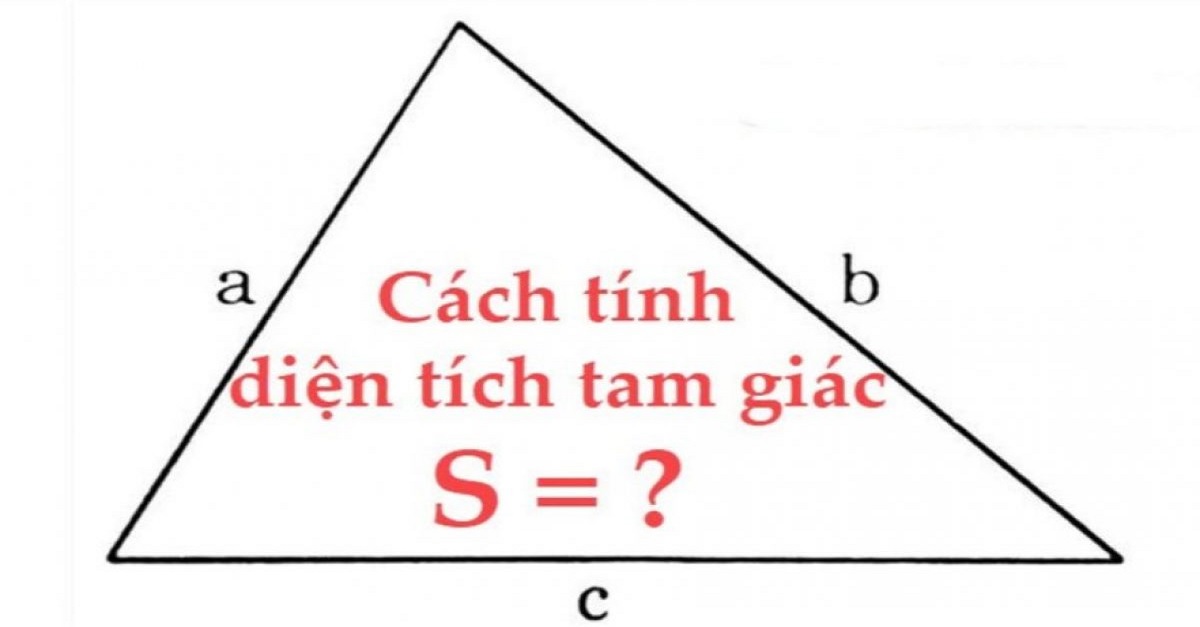
Vậy thực hiện cơ hội này nhằm tính diện tích S của một tam giác đều?
Để tính diện tích S của một tam giác đều, tao rất có thể dùng công thức sau: diện tích S = (cạnh)^2 * sqrt(3) / 4. Lưu ý rằng cạnh của tam giác đều là chừng nhiều năm của 3 cạnh đều bằng nhau.
1. Xác quyết định chừng nhiều năm cạnh của tam giác đều: Để tính diện tích S tam giác đều, tao cần phải biết chừng nhiều năm của một cạnh. Hãy đo hoặc xác lập chừng nhiều năm cạnh của tam giác đều tiếp tục mang đến.
2. Sử dụng công thức tính diện tích S: Sau Khi có tính nhiều năm cạnh, tao rất có thể vận dụng công thức diện tích S tam giác đều như sau. Gọi a là chừng nhiều năm của cạnh tam giác đều, tao có:
diện tích = (a^2 * sqrt(3)) / 4.
3. Thực hiện tại tính toán: Thay chừng nhiều năm cạnh (a) của tam giác đều tiếp tục mang đến vô công thức diện tích S và thể hiện sản phẩm. Đảm bảo đo lường và tính toán đúng mực với những luật lệ tính quan trọng như bình phương, căn bậc nhì và luật lệ phân chia.
Ví dụ:
Giả sử tao sở hữu một tam giác đều sở hữu chừng nhiều năm cạnh là 5cm. sát dụng công thức diện tích S tam giác đều, tao có:
diện tích = (5^2 * sqrt(3)) / 4
= (25 * 1.732) / 4
= 43.301 / 4
= 10.825 cm^2
Vậy, diện tích S của tam giác đều sở hữu cạnh chừng nhiều năm 5cm là 10.825 cm^2.
Công thức tính diện tích S tam giác đều là gì?
Công thức tính diện tích S của tam giác đều được xem vị cách:
1. Tính chừng nhiều năm cạnh tam giác: Vì tam giác đều sở hữu 3 cạnh đều bằng nhau, nên tao chỉ cần phải biết chừng nhiều năm của một cạnh có một không hai. Gọi cạnh tam giác là a.
2. Tính diện tích S tam giác: Diện tích tam giác đều được xem vị công thức: Diện tích = (cạnh^2 * căn bậc nhì của 3)/4.
Hay cách tiếp theo, tao cũng rất có thể tính diện tích S tam giác đều vị cách: Diện tích = (a^2 * căn bậc nhì của 3)/4.
3. sát dụng công thức: Gặp Việc tính diện tích S tam giác đều, tao chỉ việc thay cho a vô công thức tính diện tích S ở bước bên trên nhằm tìm ra sản phẩm sau cùng.
Ví dụ: Nếu cạnh tam giác đều là 6 đơn vị chức năng, tao thay cho a = 6 vô công thức, tao có: Diện tích = (6^2 * căn bậc nhì của 3)/4.
Tính toán nối tiếp, tao sẽ sở hữu sản phẩm sau cùng là diện tích S của tam giác đều.

_HOOK_
Xem thêm: truyện gió ấm không bằng anh thâm tình
Cách tính diện tích S hình tam giác đều
\"Bạn mong muốn lần hiểu về diện tích S hình tam giác đều? Video này tiếp tục giúp cho bạn nắm rõ về kiểu cách tính và phần mềm diện tích S vô hình tam giác. Hãy nằm trong coi nhằm mày mò những tuyệt kỹ thú vị!\"
Cách tính diện tích S hình tam giác cân nặng | toán lớp 3 4 5 7 8
\"Bạn từng vướng mắc về diện tích S hình tam giác cân? Đừng lo sợ, đoạn phim này tiếp tục trả lời toàn bộ những thắc mắc của chúng ta. Hãy nằm trong theo gót dõi nhằm biết phương pháp tính diện tích S và vận dụng vô những Việc thực tiễn.\"
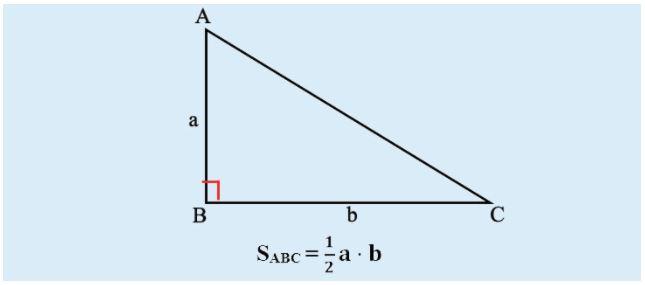
Tam giác đều sở hữu lối cao ra sao và tầm quan trọng của chính nó là gì trong các việc tính diện tích?
Trong tam giác đều, lối cao là 1 trong đường thẳng liền mạch được vẽ kể từ đỉnh của tam giác cho tới lòng sao mang đến vuông góc với lòng. Đường cao này tách lòng trở thành nhì đoạn có tính nhiều năm đều bằng nhau, dẫn đến nhì tam giác cân đối nhau.
Vai trò của lối cao trong các việc tính diện tích S tam giác đều là cực kỳ cần thiết. Đường cao đó là lối cao của những tam giác cân nặng bao gồm tam giác đều. Khi tính diện tích S tam giác đều, tất cả chúng ta dùng công thức diện tích S của tam giác cân nặng.
Công thức diện tích S tam giác cân nặng là S = 50% * b * h, vô bại liệt S là diện tích S tam giác, b là chừng nhiều năm lòng và h là chừng nhiều năm lối cao.
Trong tam giác đều, nhì đoạn lòng được dẫn đến vị lối cao đều sở hữu chừng nhiều năm đều bằng nhau, điều này Tức là lòng và lối cao nằm trong phân chia song tam giác trở thành nhì miền sở hữu diện tích S đều bằng nhau. Do bại liệt, tao rất có thể tính diện tích S tam giác đều bằng phương pháp nhân diện tích S của một miếng nửa tam giác với 2.
Vì tam giác đều sở hữu những cạnh đều bằng nhau, tao rất có thể đo lường và tính toán chừng nhiều năm lòng hoặc lối cao bằng phương pháp dùng công thức Pythagore. Với tam giác đều sở hữu chừng nhiều năm cạnh a, tao rất có thể tính chừng nhiều năm lòng hoặc lối cao là h = (√3/2) * a.
Tổng kết lại, lối cao vô tam giác đều sở hữu tầm quan trọng cần thiết trong các việc tính diện tích S tam giác. Công thức diện tích S tam giác cân nặng (1/2 * b * h) vận dụng mang đến tam giác đều với lòng và lối cao có tính nhiều năm đều bằng nhau. Đường cao tách tam giác đều trở thành nhì miền sở hữu diện tích S đều bằng nhau, được chấp nhận tính diện tích S tam giác đều vị nửa diện tích S tam giác cân nặng và nhân với 2.
Nếu biết lối cao của tam giác đều, làm thế nào tính được diện tích S tam giác đều?
Để tính diện tích S của tam giác đều, tao rất có thể dùng chừng nhiều năm của lối cao của tam giác đều. Đường cao của tam giác đều phân chia tam giác trở thành nhì tam giác vuông cân nặng tuy nhiên sở hữu tam giác vuông vuông góc bên trên đỉnh.
Bước 1: Đo lối cao của tam giác đều. Đường cao là lối liên kết kể từ đỉnh của tam giác cho tới lối thân thích lòng tam giác và vuông góc với lòng.
Bước 2: Tính chừng nhiều năm lối cao bằng phương pháp dùng Định lí Pythagoras. Định lí này cho thấy rằng vô một tam giác vuông, bình phương của chừng nhiều năm lối cao vị tích của nhì cạnh góc vuông.
Bước 3: Tính diện tích S của tam giác đều bằng phương pháp nhân chừng nhiều năm lối cao với chừng nhiều năm của lòng tam giác và phân chia mang đến 2. Công thức này được ghi chép lừng danh như S = 0.5 * b * h, vô bại liệt S là diện tích S tam giác, b là chừng nhiều năm của lòng tam giác và h là chừng nhiều năm của lối cao.
Ví dụ: Giả sử lối cao của tam giác đều là 5 centimet. Đáy tam giác có tính nhiều năm là 8 centimet.
Sử dụng công thức diện tích S tam giác, thay cho vô độ quý hiếm của b và h, tao có:
S = 0.5 * 8 * 5
S = đôi mươi cm^2
Vậy diện tích S của tam giác đều vô tình huống này là đôi mươi cm^2.
Lưu ý rằng diện tích S của tam giác đều tiếp tục thay cho thay đổi tùy từng chừng nhiều năm của lối cao và lòng tam giác. Trong tình huống tam giác đều sở hữu chừng nhiều năm cạnh đều nhau, tao rất có thể dùng công thức giản dị S = a^2 * (sqrt(3) / 4), vô bại liệt a là chừng nhiều năm của cạnh tam giác.
Diện tích tam giác đều sở hữu tỷ trọng ra sao với chừng nhiều năm cạnh của nó?
Diện tích tam giác đều sở hữu tỷ trọng như sau:
- Giả sử chừng nhiều năm từng cạnh của tam giác đều là a.
- Để tính diện tích S tam giác đều, tao dùng công thức: Diện tích = (a^2 * √3) / 4
- Với chừng nhiều năm cạnh a, diện tích S tam giác đều tiếp tục tỷ trọng với căn bậc nhì của bình phương chừng nhiều năm cạnh theo gót công thức nêu bên trên.
- Vấn đề này Tức là nếu như tao tăng mức độ nhiều năm cạnh của tam giác đều gấp hai, diện tích S của chính nó tiếp tục tăng vội vàng tứ đợt (2^2 = 4).
- Tương tự động, nếu như tao tách chừng nhiều năm cạnh của tam giác đều xuống 1/2, diện tích S của chính nó tiếp tục giảm sút một phân nửa (1/2^2 = 1/4).
- Tỷ lệ này lưu giữ ko thay đổi mang đến toàn bộ những tam giác đều, vì như thế toàn bộ đều sở hữu những cạnh đều bằng nhau.
Tam giác đều sở hữu phần mềm vô nghành nghề này của cuộc sống thường ngày mặt hàng ngày?
Tam giác đều sở hữu phần mềm thoáng rộng vô cuộc sống thường ngày hằng ngày, nhất là vô nghành nghề design và kiến thiết. Dưới đó là một vài phần mềm ví dụ của tam giác đều vô cuộc sống thường ngày mặt hàng ngày:
1. Mặt bàn tam giác đều: Một số mặt mày bàn vô mái ấm gia đình hoặc điểm thao tác được design bên dưới dạng tam giác đều nhằm tận dụng tối đa không khí và dẫn đến một cảm hứng tiến bộ và khác biệt.
2. Thiết tiếp đèn tam giác đều: Thiết bị phát sáng sở hữu dạng tam giác đều thông thường được dùng nhằm tô điểm không khí thiết kế bên trong và tạo nên điểm vượt trội mang đến căn chống.
3. Thiết tiếp đồ dùng trang sức: Một số loại vòng cổ, phiên bản lề và trang sức đẹp không giống sở hữu dạng tam giác đều muốn tạo đi ra vẻ nước ngoài hình thẩm mỹ và làm đẹp và sự tinh tế và sắc sảo.
4. Kiến trúc xây dựng: Tam giác đều được dùng vô phong cách thiết kế nhằm tạo thành những dự án công trình phổ biến. Ví dụ phổ biến nhất là Pyramids của Ai Cập, được kiến thiết dựa vào dáng vẻ tam giác đều.
5. Ngành công nghiệp dù tô: Một số khuôn xe pháo xe hơi sở hữu dáng vẻ tam giác đều, nhất là vô phần trước của xe pháo, nhằm mục tiêu tạo nên chừng bằng phẳng và tăng tính thẩm mỹ và làm đẹp.
6. Trò đùa và giáo dục: Tam giác đều cũng khá được dùng trong những trò đùa, romes và những sinh hoạt dạy dỗ nhằm cải cách và phát triển suy nghĩ hình học tập và logic của trẻ nhỏ.
Như vậy, tam giác đều sở hữu nhiều phần mềm vô cuộc sống thường ngày hằng ngày và được dùng phát minh trong vô số nghành nghề không giống nhau.

Xem thêm: thế nào là phát triển bền vững
Tam giác đều và tam giác thông thường không giống nhau ra sao trong các việc tính diện tích?
Tam giác đều và tam giác thông thường không giống nhau trong các việc tính diện tích S cũng chính vì phương pháp tính diện tích S của bọn chúng sở hữu một vài điểm không giống nhau cơ phiên bản.
Đối với tam giác thông thường, tất cả chúng ta rất có thể dùng công thức Heron nhằm tính diện tích S. Công thức này dựa vào chừng nhiều năm những cạnh của tam giác. Gọi a, b, và c theo thứ tự là chừng nhiều năm tía cạnh của tam giác, tao rất có thể dùng công thức sau nhằm tính diện tích S tam giác:
diện tích = √(s(s-a)(s-b)(s-c))
trong bại liệt s là nửa chu vi của tam giác và được xem bằng phương pháp công thức:
s = (a + b + c)/2
Trong Khi bại liệt, so với tam giác đều, phương pháp tính diện tích S giản dị rộng lớn. Bởi vì như thế tam giác đều sở hữu tía cạnh đều bằng nhau, tất cả chúng ta chỉ việc tính diện tích S xứng đáng như sau:
diện tích = (√3/4) * a^2
trong bại liệt a là chừng nhiều năm cạnh của tam giác.
Tóm lại, phương pháp tính diện tích S của tam giác đều và tam giác thông thường sở hữu những khác lạ về công thức tính như và được reviews bên trên.
_HOOK_
Cách tính diện tích S tam giác tổng quát tháo (tam giác thông thường, tam giác vuông) Toán lớp 5
\"Diện tích tam giác tổng quát tháo là yếu tố khá phức tạp? Đừng phiền lòng, đoạn phim này tiếp tục giúp cho bạn từng bước hiểu về kiểu cách tính và phần mềm diện tích S tam giác tổng quát tháo vô những Việc thực tiễn. Hãy nằm trong coi nhằm phanh đi ra những kỹ năng và kiến thức mới!\"











Bình luận