Trọng tâm của tam giác là 1 trong những trong mỗi kiến thức và kỹ năng rất rất cần thiết và thịnh hành trong mỗi năm học tập phổ thông. Bài ghi chép tiếp sau đây, Quantrimang.com van nài reviews với chúng ta những kiến thức và kỹ năng tương quan cho tới trọng tâm tam giác, công thức tính trọng tâm tam giác, công thức tính tọa phỏng trọng tam giác, chào chúng ta xem thêm nhằm phần mềm nhập giải những vấn đề nhập quy trình học hành nhé.
Trọng tâm là gì?
Một tam giác sở hữu 3 lối trung tuyến, đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập.
Bạn đang xem: tính chất trọng tâm tam giác
Trọng tâm của tam giác là uỷ thác điểm của phụ thân lối trung tuyến.
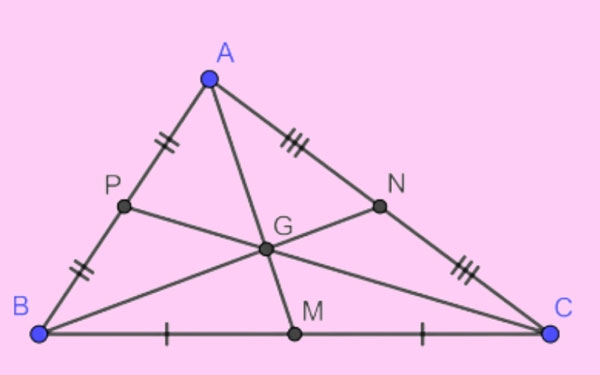
Tính hóa học của trọng tâm nhập tam giác
Khoảng cơ hội kể từ trọng tâm của tam giác cho tới đỉnh vì chưng 2/3 phỏng lâu năm lối trung tuyến ứng với đỉnh bại liệt.
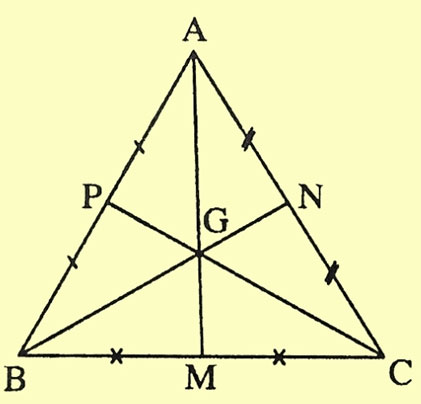
Tam giác ABC, với những lối trung tuyến AM, BN, CP và trọng tâm G, tớ có:
- GA = 2/3 AM
- GB = 2/3 BN
- GC = 2/3 CP

Trọng tâm tam giác vuông
Trọng tâm của tam giác vuông cũng rất được xác lập tựa như trọng tâm của tam giác thông thường.
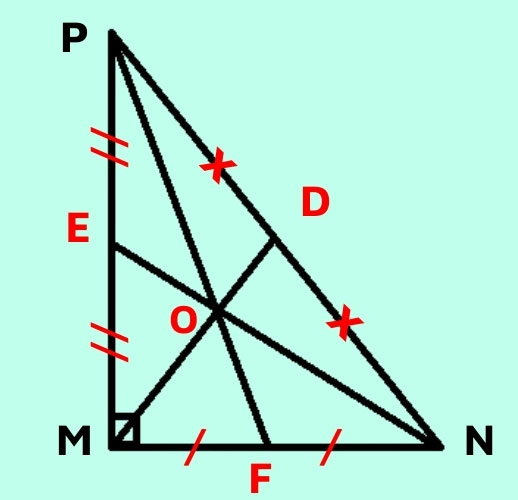
Tam giác MNP vuông bên trên M.
3 lối trung tuyến MD, NE, PF uỷ thác nhau bên trên trọng tâm O. Ta sở hữu MD là trung tuyến của góc vuông PMN nên MD = một nửa PN = DP = Doanh Nghiệp.
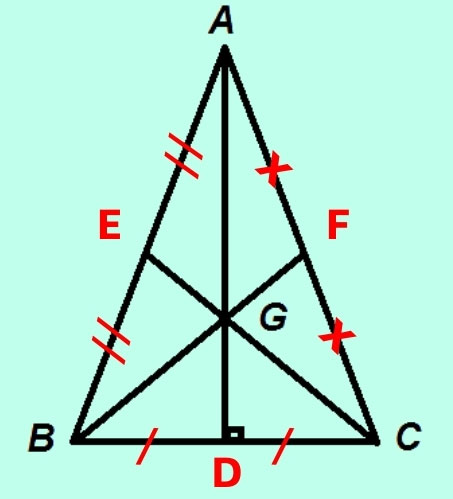
Trọng tâm tam giác cân
Tam giác ABC cân nặng bên trên A, sở hữu G là trọng tâm.
Vì tam giác ABC cân nặng bên trên A nên AG vừa vặn là lối trung tuyến, lối cao và là lối phân giác, kể từ bại liệt tớ suy rời khỏi được hệ ngược của trọng tâm tam giác cân nặng ABC như sau:
- Góc BAD vì chưng góc CAD.
- Trung tuyến AD vuông góc với cạnh lòng BC.
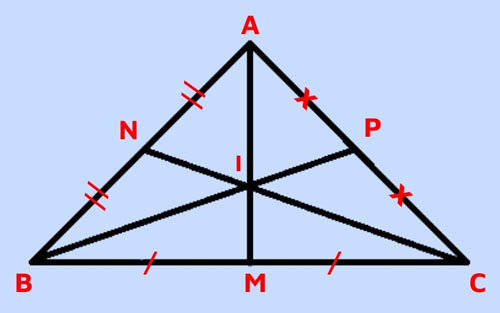
Trọng tâm của tam giác vuông cân
Có tam giác ABC vuông cân nặng bên trên A và I là trọng tâm. AM là lối trung trực, lối trung tuyến và lối cao của tam giác này nên AM vuông góc với BC.
Mặt không giống, vì như thế tam giác ABC vuông cân nặng bên trên A nên:
AB = AC.
=> BP = công nhân và BN = AN = CP = AP.
Trọng tâm tam giác đều
Tam giác ABC đều, G là uỷ thác điểm phụ thân lối trung tuyến, lối cao, lối phân giác.
Vì vậy bám theo đặc điểm của tam giác đều tớ sở hữu G vừa vặn là trọng tâm, trực tâm, tâm lối tròn xoe nước ngoài tiếp và nội tiếp của tam giác ABC.
Cách mò mẫm trọng tâm tam giác
Cách 1: Giao điểm 3 lối trung tuyến
Xác lăm le trọng tâm tam giác bằng phương pháp lấy uỷ thác điểm của phụ thân lối trung tuyến.
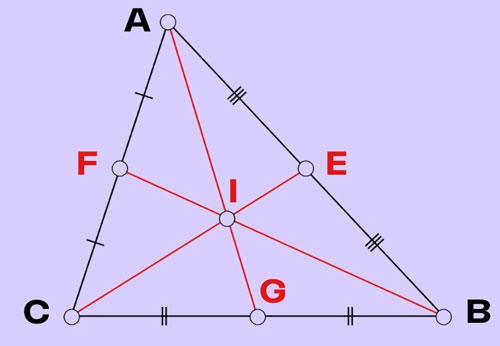
Bước 1: Vẽ tam giác ABC, thứu tự xác lập trung điểm của những cạnh AB, BC, CA.
Bước 2: Nối thứu tự những đỉnh cho tới trung điểm của cạnh đối lập. Nối A với G, B với F, C với E.
Bước 3: Giao điểm I của phụ thân lối trung tuyến là AG, BF, CE là trọng tâm của tam giác ABC.
Cách 2: Tỉ lệ bên trên lối trung tuyến
Xác lăm le trọng tâm tam giác dựa vào tỉ lệ thành phần lối trung tuyến.
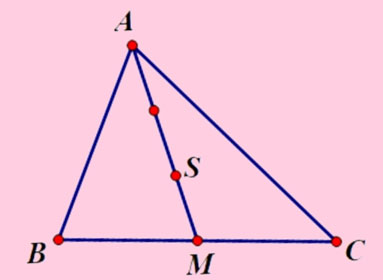
Bước 1: Vẽ tam giác ABC, xác lập trung điểm M của cạnh BC.
Bước 2: Nối đỉnh A với trung điểm M, tiếp sau đó lấy điểm S sao mang lại AS = 2/3 AM.
Theo tính chất trọng tâm tam giác thì điểm S đó là trọng tâm tam giác ABC.
Xem thêm: giải pháp bảo vệ môi trường
Bài tập luyện về trọng tâm tam giác
Bài 1:
Tam giác ABC sở hữu trung tuyến AD = 9cm và trọng tâm I. Tính phỏng lâu năm đoạn AI?
Giải:
Ta sở hữu I là trọng tâm của tam giác ABC và AD là lối trung tuyến nên AI = (2/3) AD (theo đặc điểm phụ thân lối trung tuyến của tam giác).
Do đó: AG = (2/3).9 = 6 (cm).
Vậy đọan AI có tính lâu năm 6 centimet.
Bài 2:
Cho I là trọng tâm của tam giác đều MNP. Chứng minh rằng: IM = IN = IP.
Giải:
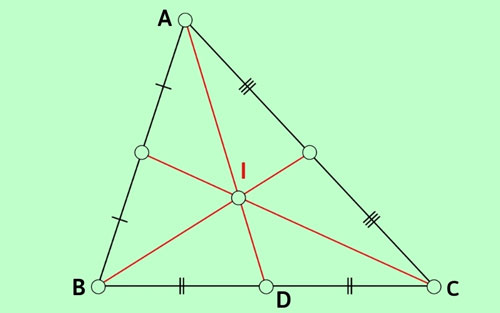
Gọi trung điểm MN, MP, PN thứu tự là R, O, S.
Khi bại liệt MS, quảng cáo, NO đồng quy bên trên trọng tâm I.
Ta sở hữu ∆MNP đều, suy ra:
MS = quảng cáo = NO (1).
Vì I là trọng tâm của ∆ABC nên bám theo đặc điểm lối trung tuyến:
MI = 2/3 MS, PI = 2/3 quảng cáo, NI = 2/3 NO (2).
Từ (1) , (2) ⇒ GA = GB = GC.

Tọa phỏng của trọng tâm tam giác nhập mặt mũi phẳng lì Oxy
Cho tam giác ABC sở hữu A(xA; yA), B(xB; yB), C(xC; yC). Nếu G là trọng tâm của tam giác ABC thì:

Ví dụ 1: Trong mặt mũi phẳng lì tọa phỏng Oxy, cho những điểm A(2; 0), B(0; 4), C(1; 3).
a, Chứng minh rằng A, B, C là 3 đỉnh của một tam giác.
b, Tìm tọa phỏng nhập tâm tam giác ABC.
Hướng dẫn giải:
a, Ta có: ![]() =(-2; 4) và
=(-2; 4) và ![]() =(-1; 3)
=(-1; 3)
Do ![]() nên
nên ![]() không nằm trong phương, suy rời khỏi A, B, C ko trực tiếp mặt hàng.
không nằm trong phương, suy rời khỏi A, B, C ko trực tiếp mặt hàng.
Vậy A, B, C là 3 đỉnh của một tam giác.
b, Gọi G là trọng tâm tam giác ABC. Suy rời khỏi tọa phỏng của G là:
Xem thêm: các chất điện li yếu

Vậy tọa phỏng trọng tâm tam giác ABC là G (1; ![]() ).
).
Ngoài định nghĩa và những công thức về trọng tâm tam giác phía trên, những bạn cũng có thể mò mẫm hiểu thêm thắt những kiến thức và kỹ năng không giống về tam giác như diện tích S tam giác, chu vi tam giác, lối cao tam giác.












Bình luận