Chủ đề Công thức tính cạnh huyền tam giác vuông lớp 5: Công thức tính cạnh huyền tam giác vuông lớp 5 là 1 trong kiến thức và kỹ năng cần thiết hùn những em học viên nắm rõ và vận dụng nhập những Việc. Nhờ công thức này, tất cả chúng ta hoàn toàn có thể đơn giản và dễ dàng tính được chừng nhiều năm cạnh huyền chỉ với vấn đề về chừng nhiều năm những cạnh góc vuông. Như vậy hùn những em mạnh mẽ và tự tin và thuận tiện trong công việc giải toán và thực hiện bài xích tập dượt về tam giác vuông.
Công thức tính cạnh huyền tam giác vuông lớp 5 là gì?
Công thức tính cạnh huyền tam giác vuông nhập lớp 5 là công thức Pythagoras, được links với tam giác vuông và những cạnh của chính nó.
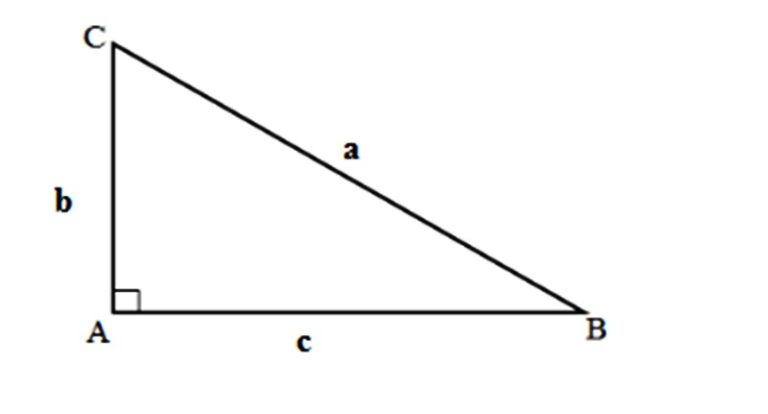
Theo công thức Pythagoras, nhằm tính cạnh huyền của tam giác vuông, tớ cần phải biết nhì cạnh góc vuông (các cạnh góc vuông là những cạnh ở Chịu lòng của tam giác) của tam giác. Gọi những cạnh góc vuông ứng là a và b, cạnh huyền là c.
Công thức Pythagoras mang lại tớ hiểu được c^2 = a^2 + b^2. Nghĩa là bình phương của cạnh huyền vì như thế tổng bình phương của nhì cạnh góc vuông.
Để tính cạnh huyền, tớ lấy căn bậc nhì của phương trình c^2 = a^2 + b^2.
Ví dụ: Nếu tớ với nhì cạnh góc vuông có tính nhiều năm là 3 và 4, tớ hoàn toàn có thể tính cạnh huyền bằng phương pháp tiến hành công việc sau:
- sít dụng công thức Pythagoras: c^2 = 3^2 + 4^2 = 9 + 16 = 25.
- Lấy căn bậc nhì của phương trình: c = √25 = 5.
Vậy nên, công thức tính cạnh huyền tam giác vuông nhập lớp 5 là c^2 = a^2 + b^2 và c = √(a^2 + b^2).
Bạn đang xem: tính cạnh huyền tam giác vuông
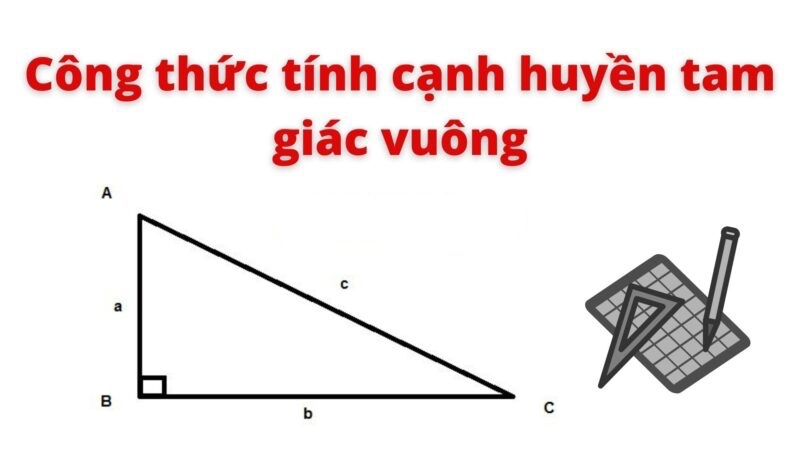
Tam giác vuông quan trọng đặc biệt với cạnh huyền vì như thế bao nhiêu?
The length of the hypotenuse (cạnh huyền) of a special right triangle with sides following the Pythagorean triple is calculated using the formula c = √(a² + b²). For example, in a triangle with sides measuring 3, 4, and 5, the hypotenuse is calculated as c = √(3² + 4²) = √(9 + 16) = √25 = 5. Therefore, the length of the hypotenuse in this case is 5.
Liên hệ của cạnh huyền với những cạnh không giống của tam giác vuông như vậy nào?
Liên hệ của cạnh huyền với những cạnh không giống của tam giác vuông được xác lập vì như thế Định lý Pythagoras. Định lý này bảo rằng bình phương của chừng nhiều năm cạnh huyền vì như thế tổng bình phương của nhì cạnh góc vuông.
Cụ thể, nếu như a và b là chừng nhiều năm của nhì cạnh góc vuông của tam giác vuông và c là chừng nhiều năm của cạnh huyền, thì công thức tính cạnh huyền là:
c² = a² + b²
Điều này Tức là, nhằm tính chừng nhiều năm của cạnh huyền, tớ lấy căn bậc nhì của tổng bình phương của nhì cạnh góc vuông.
Ví dụ, nếu như nhì cạnh góc vuông có tính nhiều năm là 3 và 4, tớ hoàn toàn có thể tính chừng nhiều năm của cạnh huyền bằng phương pháp vận dụng công thức trên:
c² = 3² + 4² = 9 + 16 = 25
Do bại, chừng nhiều năm của cạnh huyền là căn bậc nhì của 25, tức là 5.
Qua bại, tất cả chúng ta hoàn toàn có thể Kết luận rằng tương tác thân thích cạnh huyền và những cạnh không giống của tam giác vuông được xác lập vì như thế Định lý Pythagoras và công thức tính cạnh huyền là c² = a² + b².
Cạnh Huyền Là Gì - 3 Cách Tính Cạnh Huyền Tam Giác Vuông - Toán Học
\"Cạnh Huyền Tam Giác Vuông\": Đến và mày mò bí hiểm của cạnh huyền tam giác vuông, một mày mò nhân tài toán học tập. Video này tiếp tục khiến cho bạn làm rõ rộng lớn về công thức tính cạnh huyền và phần mềm của chính nó nhập cuộc sống thực.\"
Bình phương của số đo cạnh huyền vì như thế công thức nào?
Công thức tính bình phương của số đo cạnh huyền nhập tam giác vuông là toan lý Pythagoras. Theo công thức này, bình phương của số đo cạnh huyền vì như thế tổng bình phương của nhì cạnh góc vuông sót lại. Như vậy được màn biểu diễn như sau: cạnh huyền² = cạnh loại nhất² + cạnh loại hai². Với tam giác vuông ABC, nhập bại AB và BC là nhì cạnh góc vuông, công thức này được xem là c² = a² + b². Để tính được cạnh huyền, tớ hoàn toàn có thể lấy căn bậc nhì của tổng bình phương của nhì cạnh góc vuông, tức là c = √(a² + b²).
Công thức tính cạnh huyền tam giác vuông là gì?
Công thức tính cạnh huyền tam giác vuông là công thức Pythagoras và được màn biểu diễn bên dưới dạng c² = a² + b² hoặc c = √(a² + b²). Trong số đó, c là cạnh huyền tam giác vuông, và a, b là nhì cạnh góc vuông của tam giác vuông bại. Để tính cạnh huyền tam giác vuông, tớ chỉ việc thay cho độ quý hiếm của a, b nhập công thức bên trên và đo lường và tính toán.
_HOOK_
Xem thêm: giải pháp bảo vệ môi trường
Cạnh huyền là gì nhập tam giác vuông?
Cạnh huyền là cạnh đối lập với góc vuông nhập tam giác vuông. Ta hoàn toàn có thể dùng toan lý Pythagoras nhằm tính chừng nhiều năm cạnh huyền của tam giác vuông. Định lý Pythagoras bảo rằng bình phương của cạnh huyền (c) vì như thế tổng bình phương của nhì cạnh góc vuông (a và b). Công thức tính cạnh huyền tam giác vuông là: c² = a² + b². Với công thức này, tất cả chúng ta hoàn toàn có thể tính được chừng nhiều năm cạnh huyền của tam giác vuông lúc biết chừng nhiều năm nhì cạnh góc vuông.
Tính Cạnh Huyền Trong Tam Giác Vuông
\"Công thức tính cạnh huyền\": Quý khách hàng hoảng loạn với công thức tính cạnh huyền? Đừng bồn chồn, Clip này tiếp tục dạy dỗ các bạn một cơ hội dễ dàng nắm bắt phương pháp tính cạnh huyền của một tam giác vuông. Hãy nằm trong mày mò và vận dụng kiến thức và kỹ năng nhập thực tế!
Tam giác vuông với từng nào cạnh?
Tam giác vuông với tía cạnh.

Làm thế này nhằm tính được cạnh huyền của tam giác vuông?
Để tính được cạnh huyền của tam giác vuông, tất cả chúng ta hoàn toàn có thể dùng toan lý Pythagoras. Định lý này bảo rằng bình phương của cạnh huyền vì như thế tổng bình phương của nhì cạnh góc vuông.
Công thức tính cạnh huyền tam giác vuông là: c = √(a² + b²).
Trong đó:
- a và b là chừng nhiều năm nhì cạnh góc vuông của tam giác vuông.
- c là chừng nhiều năm cạnh huyền của tam giác vuông.
Ví dụ, fake sử tất cả chúng ta với tam giác vuông với nhì cạnh góc vuông có tính nhiều năm thứu tự là 3 và 4. Để tính chừng nhiều năm cạnh huyền, tất cả chúng ta tiến hành công việc sau:
1. Tính tổng bình phương của nhì cạnh góc vuông: 3² + 4² = 9 + 16 = 25.
2. Lấy căn bậc nhì của tổng trên: √25 = 5.
Vậy chừng nhiều năm cạnh huyền của tam giác vuông là 5.
Tam giác vuông với từng nào loại cạnh?
Tam giác vuông với 3 loại cạnh chủ yếu, bao hàm cạnh góc vuông (hay cạnh huyền), cạnh góc nhọn và cạnh góc tù.
- Cạnh góc vuông (hay cạnh huyền) là cạnh ở đối lập với góc vuông nhập tam giác vuông. Cạnh này còn có chừng nhiều năm là số thực dương và được ký hiệu là c.
- Cạnh góc nhọn là cạnh ở kề với góc nhọn nhập tam giác vuông. Cạnh này còn có chừng nhiều năm là số thực dương và được ký hiệu là a hoặc b.
- Cạnh góc tù là cạnh ở đối lập với góc tù nhập tam giác vuông. Cạnh này còn có chừng nhiều năm là số thực dương và được ký hiệu là a hoặc b.
Với tam giác vuông, cạnh góc vuông (cạnh huyền) luôn luôn là cạnh nhiều năm nhất nhập tam giác và được xem vì như thế công thức Pythagoras: c = √(a² + b²), nhập bại a và b là chừng nhiều năm nhì cạnh sót lại và c² là bình phương chừng nhiều năm cạnh góc vuông.
Tóm lại, tam giác vuông có một cạnh góc vuông (cạnh huyền) và 2 cạnh góc nhọn hoặc cạnh góc tù.
Xem thêm: at the moment là thì gì
.jpg)
Sự tương tác thân thích cạnh huyền và những góc nhập tam giác vuông như vậy nào?
Sự tương tác thân thích cạnh huyền và những góc nhập tam giác vuông được tế bào miêu tả vì như thế toan lý Pythagoras. Định lý này xác định rằng nhập một tam giác vuông, bình phương của cạnh huyền vì như thế tổng bình phương của nhì cạnh góc vuông.
Hãy fake sử nhập tam giác vuông ABC, AB là cạnh huyền, và AC, BC thứu tự là nhì cạnh góc vuông. Định lý Pythagoras tế bào miêu tả sự tương tác thân thích bọn chúng như sau:
AB² = AC² + BC²
Đây là 1 trong công thức cần thiết Lúc đo lường và tính toán những độ quý hiếm nhập tam giác vuông. bằng phẳng cơ hội biết chừng nhiều năm nhì cạnh góc vuông, tớ hoàn toàn có thể tính được chừng nhiều năm của cạnh huyền.
Ví dụ, nếu như tớ biết chừng nhiều năm AC và BC thứu tự là 3 và 4, tớ hoàn toàn có thể tính chừng nhiều năm của AB như sau:
AB² = 3² + 4²
AB² = 9 + 16
AB² = 25
Do bại, AB = √25 = 5.
Vậy chừng nhiều năm của cạnh huyền AB là 5.
_HOOK_











.jpg)

Bình luận