Chủ đề Khái niệm nhị tam giác đồng dạng: Khái niệm nhị tam giác đồng dạng là 1 trong những phần cần thiết vô bài học kinh nghiệm Toán lớp 8, hùn học viên hiểu và phần mềm trong các công việc giải những bài bác tập dượt. Việc nắm rõ định nghĩa này hùn học viên nâng lên khả năng nhận ra và đo lường những tam giác đồng dạng, kể từ cơ nâng cấp năng lực giải toán và xây cất hạ tầng lý thuyết vững chãi. Cùng với việc chỉ dẫn của những nghề giáo và tư liệu học tập tương thích, học viên tiếp tục dễ dàng và đơn giản thu nhận và vận dụng kỹ năng và kiến thức này một cơ hội hiệu suất cao.
Loigiaihay.com: Hai tam giác được xem là đồng dạng như vậy nào?
Hai tam giác A\'B\'C\' được xem là đồng dạng với tam giác ABC nếu như đem tía fake thiết sau:
1. Hai cặp góc ứng của nhị tam giác vày nhau: Góc \\(\\widehat{A} = \\widehat{A\'}\\), góc \\(\\widehat{B} = \\widehat{B\'}\\) và góc \\(\\widehat{C} = \\widehat{C\'}\\).
2. Tỉ số phỏng lâu năm những cạnh ứng của nhị tam giác vày nhau: \\(\\frac{AB}{A\'B\'} = \\frac{BC}{B\'C\'} = \\frac{AC}{A\'C\'}\\).
3. Tương tự động như bên trên, tỉ số phỏng lâu năm những đỉnh ứng của nhị tam giác vày nhau: \\(\\frac{DA}{D\'A\'} = \\frac{DB}{D\'B\'} = \\frac{DC}{D\'C\'}\\) (nếu có).
Nếu tía fake thiết bên trên vừa lòng, tao hoàn toàn có thể Kết luận rằng nhị tam giác ABC và A\'B\'C\' đồng dạng.
Bạn đang xem: tỉ số diện tích của hai tam giác đồng dạng
Khái niệm nhị tam giác đồng dạng là gì?
Khái niệm nhị tam giác đồng dạng là sự việc nhị tam giác đem và một tỷ trọng Một trong những 2 lần bán kính tam giác hoặc những đoạn trực tiếp ứng. Vấn đề này tức là những góc ứng vô nhị tam giác đồng dạng sẽ sở hữu được nằm trong độ quý hiếm.
Cụ thể, nhằm nhị tam giác ABC và A\'B\'C\' là đồng dạng:
1. Tam giác ABC và A\'B\'C\' cần đem những cạnh ứng AB và A\'B\', BC và B\'C\', AC và A\'C\' đang được kéo dãn dài trở thành đường thẳng liền mạch.
2. Tỉ lệ Một trong những cạnh ứng của nhị tam giác cần đều bằng nhau. Vấn đề này hoàn toàn có thể được màn biểu diễn như sau: AB / A\'B\' = BC / B\'C\' = AC / A\'C\'.
3. Các góc ứng vô nhị tam giác cũng cần đều bằng nhau. Vấn đề này hoàn toàn có thể được màn biểu diễn như sau: góc A vày góc A\', góc B vày góc B\', góc C vày góc C\'.
Khi nhị tam giác đồng dạng, tỷ trọng Một trong những cạnh và những góc của bọn chúng sẽ không còn thay cho thay đổi. Vấn đề này khá hữu dụng trong các công việc giải quyết và xử lý những Việc tương quan cho tới tỷ trọng và hình học tập nhị tam giác.
Các ĐK nhằm nhị tam giác được cho rằng đồng dạng?
Hai tam giác được cho rằng đồng dạng nếu như vừa lòng những ĐK sau đây:
1. Điều khiếu nại cạnh-cạnh: Hai tam giác đem nhị cạnh ứng giống hệt tỷ trọng cùng nhau. Tức là chiều lâu năm của nhị cạnh ứng đem tỉ trọng đều bằng nhau.
2. Điều khiếu nại cạnh-góc-cạnh: Hai tam giác mang 1 cặp cạnh ứng giống hệt tỷ trọng và đôi khi đem cặp góc ứng đồng đều bằng nhau.
3. Điều khiếu nại góc-góc: Hai tam giác mang 1 cặp góc ứng đồng đều bằng nhau.
Khi cả tía ĐK bên trên được vừa lòng, tao hoàn toàn có thể Kết luận rằng nhị tam giác này là đồng dạng. Đây là những ĐK cơ bạn dạng nhằm xác lập tính đồng dạng của nhị tam giác.
Tam giác ABC và tam giác A\'B\'C\' được xem là đồng dạng Lúc nào?
Tam giác ABC và tam giác A\'B\'C\' được xem là đồng dạng Lúc những góc ứng của nhị tam giác cơ đều bằng nhau và tỷ trọng những cạnh ứng cũng đều bằng nhau. Cụ thể, tao đem những ĐK tại đây nhằm nhị tam giác là đồng dạng:
1. Hai góc ứng của nhị tam giác đồng dạng vày nhau: Góc A của tam giác ABC tiếp tục ứng với góc A\' của tam giác A\'B\'C\'. Góc B tiếp tục ứng với góc B\', và góc C tiếp tục ứng với góc C\'. Khi những góc này đều bằng nhau, tao đem ĐK góc A = góc A\', góc B = góc B\', và góc C = góc C\'.
2. Tỷ lệ những cạnh ứng của nhị tam giác đồng dạng vày nhau: Chiều lâu năm cạnh AB của tam giác ABC tiếp tục ứng với chiều lâu năm cạnh A\'B\' của tam giác A\'B\'C\'. Chiều lâu năm cạnh BC ứng với cạnh B\'C\', và cạnh AC ứng với cạnh A\'C\'. Khi tỷ trọng Một trong những cạnh này đều bằng nhau, tao đem ĐK AB/A\'B\' = BC/B\'C\' = AC/A\'C\'.
Khi đôi khi vừa lòng cả nhị ĐK bên trên, tao nói theo một cách khác rằng tam giác ABC và tam giác A\'B\'C\' đồng dạng. Vấn đề này cũng hoàn toàn có thể được viết lách lại trở thành khái niệm chủ yếu thức: Tam giác A\'B\'C\' được xem là đồng dạng với tam giác ABC nếu như góc ứng đều bằng nhau và tỷ trọng những cạnh ứng đều bằng nhau.
Khái niệm nhị tam giác đồng dạng - Bài 4 - Toán học tập 8 - Cô Phạm Thị Huệ Chi
\"Dễ hiểu và đồng dạng, đoạn Clip này khiến cho bạn nắm rõ rộng lớn về định nghĩa đồng dạng vô toán học tập và cơ hội vận dụng vô những bài bác tập dượt thú vị.\"
Toán học tập lớp 8 - Bài 4 - Khái niệm nhị tam giác đồng dạng
\"Bạn đang được học tập toán lớp 8? Video này tiếp tục khiến cho bạn nắm rõ những kỹ năng và kiến thức căn bạn dạng và chỉ dẫn giải những bài bác tập dượt toán thú vị vô công tác toán học tập lớp 8.\"
Điều khiếu nại cần thiết và đầy đủ nhằm nhị tam giác đồng dạng?
Điều khiếu nại cần thiết và đầy đủ nhằm nhị tam giác đồng dạng là:
1. Hai tam giác cần đem và một góc ở đỉnh: Trong nhị tam giác đồng dạng, những góc ở đỉnh ứng của bọn chúng cần đều bằng nhau. Nếu nhị góc ở đỉnh của nhị tam giác là đều bằng nhau, tao hoàn toàn có thể Kết luận rằng nhị tam giác cơ đồng dạng.
2. Hai cặp cạnh ứng của nhị tam giác cần đem tỷ số vày nhau: Để nhị tam giác đồng dạng, tỷ số phỏng lâu năm nhị cạnh ứng của bọn chúng cần đều bằng nhau. Vấn đề này tức là nếu như tao lấy một cạnh của tam giác loại nhất và phân tách cho tới cạnh ứng của tam giác loại nhị, tỷ số cơ cần vày tỷ số của nhị cạnh ứng không giống của nhị tam giác.
3. Tam giác sót lại đem góc ko thuộc sở hữu group góc ứng cần phải có cạnh tương ứng: Trong một chuỗi tam giác đồng dạng, tam giác sót lại đem góc ko thuộc sở hữu group góc ứng cần đem cạnh ứng với cùng 1 cạnh của tam giác trước tiên vô chuỗi.
4. Tổng nhị tam giác ko thể trùng với tam giác loại tía được: Vấn đề này tức là nhị tam giác được xác lập vày nhị góc và phỏng lâu năm cạnh ứng ko thể trùng với cùng 1 tam giác loại tía đem nhị góc ứng cơ và một cạnh có tính lâu năm ứng.
Qua cơ, nhằm minh chứng nhị tam giác đồng dạng, tao cần thiết đánh giá và đối chiếu những ĐK bên trên. Nếu cả tư ĐK được vừa lòng, tao hoàn toàn có thể Kết luận rằng nhị tam giác cơ đồng dạng.

_HOOK_
Định lí không khí về nhị tam giác đồng dạng?
Định lý không khí về nhị tam giác đồng dạng là quyết định lý tế bào miêu tả về quan hệ đồng dạng thân ái nhị tam giác vô không khí tía chiều.
Định lý này nêu rõ rệt rằng nhị tam giác được gọi là đồng dạng nếu như tỉ trọng Một trong những cạnh ứng của bọn chúng đều bằng nhau và góc thân ái nhị cạnh đồng dạng (góc Một trong những cạnh tương ứng) cũng đều bằng nhau. Nói cách tiếp, nếu như tao đem nhị tam giác ABC và A\'B\'C\' vô không khí tía chiều, nhị tam giác này tiếp tục đồng dạng nếu như và chỉ nếu:
1. Các phỏng lâu năm của những cạnh ứng của nhị tam giác đem tỉ trọng đều bằng nhau. Ví dụ, tao đem AB/A\'B\' = BC/B\'C\' = AC/A\'C\'.
2. Góc thân ái nhị cạnh ứng của những tam giác cũng đều bằng nhau. Ví dụ, tao đem ∠A = ∠A\', ∠B = ∠B\', ∠C = ∠C\'.
Định lý này được cho phép tất cả chúng ta xác lập sự tương đương Một trong những hình học tập vô không khí. Nó là 1 trong những trong mỗi dụng cụ cần thiết trong các công việc giải và minh chứng những quyết định lí tương quan cho tới tam giác và những đối tượng người dùng hình học tập không giống.
Cách xác lập nhị tam giác đồng dạng vô không khí Oxyz?
Cách xác lập nhị tam giác đồng dạng vô không khí Oxyz là:
Bước 1: Dựng nhị tam giác ABC và A\'B\'C\' vô không khí Oxyz. Đảm nói rằng cả tía đỉnh của từng tam giác đều phía trên một phía phẳng phiu.
Bước 2: Kiểm tra coi những cạnh của nhị tam giác đem ứng được ko. Hai cạnh ứng cần đem tỉ trọng đều bằng nhau. Ví dụ, tao đối chiếu cạnh AB với cạnh A\'B\', cạnh AC với cạnh A\'C\', và cạnh BC với cạnh B\'C\'. Nếu tỉ trọng Một trong những cạnh ứng là đều bằng nhau, tức là AB/A\'B\' = AC/A\'C\' = BC/B\'C\', thì nhị tam giác đồng dạng.
Bước 3: Kiểm tra coi những góc của nhị tam giác đem ứng được ko. Hai góc ứng cần có tính rộng lớn đều bằng nhau. Ví dụ, tao đối chiếu góc A với góc A\', góc B với góc B\', và góc C với góc C\'. Nếu kích thước của những góc ứng là đều bằng nhau, tức là góc A = góc A\', góc B = góc B\', và góc C = góc C\', thì nhị tam giác đồng dạng.
Nếu cả nhị ĐK bên trên đều được vừa lòng, tao hoàn toàn có thể Kết luận rằng nhị tam giác ABC và A\'B\'C\' là nhị tam giác đồng dạng vô không khí Oxyz.
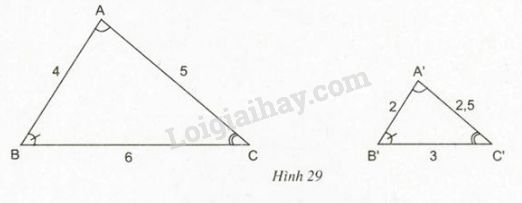
Công thức tính tỉ số với những hình tam giác đồng dạng?
Để tính tỉ số của nhị tam giác đồng dạng, tao dùng công thức sau:
Tỉ số Một trong những cạnh của nhị tam giác (đồng dạng) vày tỉ số Một trong những đoạn trực tiếp ứng của những cạnh cơ.
Chẳng hạn, cho tới tam giác ABC đồng dạng với tam giác A\'B\'C\'. Ta hoàn toàn có thể tính tỉ số của cạnh AB với cạnh A\'B\' bằng phương pháp lấy phỏng lâu năm cạnh AB phân tách cho tới phỏng lâu năm cạnh A\'B\'. Tương tự động, tao hoàn toàn có thể tính tỉ số của cạnh BC với cạnh B\'C\' và tỉ số của cạnh AC với cạnh A\'C\'.
Tổng quát mắng, tao hoàn toàn có thể viết lách công thức tỉ số như sau:
Tỉ số thân ái cạnh AB với cạnh A\'B\': AB/A\'B\'
Tỉ số thân ái cạnh BC với cạnh B\'C\': BC/B\'C\'
Tỉ số thân ái cạnh AC với cạnh A\'C\': AC/A\'C\'
Lưu ý rằng tỉ số này là ko thay đổi và được vận dụng cho tới toàn bộ những cặp cạnh ứng của nhị tam giác đồng dạng.
Ví dụ, nếu như tao đem tam giác ABC với phỏng lâu năm những cạnh thứu tự là AB = 3cm, BC = 4cm và AC = 5cm. Và tao hiểu được tam giác A\'B\'C\' đồng dạng với tam giác ABC. Nếu tao hiểu được cạnh A\'B\' ứng với cạnh AB có tính lâu năm là 2cm, tao hoàn toàn có thể tính được tỉ số thân ái cạnh AB với cạnh A\'B\':
AB/A\'B\' = 3/2 = 1.5
Tương tự động, tao hoàn toàn có thể tính tỉ số Một trong những cạnh sót lại của nhị tam giác, nhờ cơ tao hoàn toàn có thể mò mẫm rời khỏi đối sánh Một trong những cạnh của nhị tam giác đồng dạng.
Xem thêm: at the moment là thì gì
Ví dụ về sự vận dụng định nghĩa nhị tam giác đồng dạng vô giải toán thực tế?
Một ví dụ về sự vận dụng định nghĩa nhị tam giác đồng dạng vô giải toán thực tiễn là lúc tao ham muốn đo lường những độ cao thấp ko thể đo thẳng của một đối tượng người dùng.
Giả sử tất cả chúng ta mang 1 tháp cát cao, và tất cả chúng ta ham muốn xác lập độ cao của chính nó kể từ mặt mày khu đất. Vì ko thể đo thẳng độ cao của tháp cát, tất cả chúng ta hoàn toàn có thể dùng định nghĩa nhị tam giác đồng dạng nhằm giải quyết và xử lý yếu tố này.
Bước 1: Chọn một điểm A ở mặt mày khu đất và một điểm B ở đỉnh tháp cát. Đo khoảng cách kể từ điểm A cho tới tháp cát và ghi nhận độ quý hiếm là AB.
Bước 2: Tiếp bám theo, tất cả chúng ta cần thiết tạo ra một tam giác đồng dạng với tam giác ABC. Vấn đề này hoàn toàn có thể được tiến hành bằng phương pháp dịch chuyển xa xôi lên đường và kiểm soát và điều chỉnh góc nhọn loại nhị của tam giác thuở đầu.
Bước 3: Tại trên đây, tất cả chúng ta cần thiết đo khoảng cách kể từ đôi mắt phụ vương A\' cho tới địa điểm đứng của tất cả chúng ta. Vấn đề này hoàn toàn có thể được đo bằng sự việc dùng một dụng cụ đo lường và tính toán hoặc đơn giản và giản dị là dùng bước đi.
Bước 4: Cuối nằm trong, tất cả chúng ta vận dụng phương trình tỷ trọng tam giác đồng dạng nhằm đo lường độ cao của tháp cát. Ta đem biểu thức: AB/ A\'B\' = AC/ A\'C\'
Áp dụng công thức này, tất cả chúng ta hoàn toàn có thể đo lường được độ cao của tháp cát kể từ nút đôi mắt tất cả chúng ta cho tới địa điểm đứng của tất cả chúng ta.
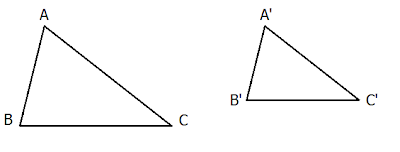
Khái niệm nhị tam giác đồng dạng - Bài 4 - Toán học tập 8 - Cô Vương Thị Hạnh
\"Chưa nắm rõ về tam giác? Video này tiếp tục lý giải cụ thể về những loại tam giác, những quyết định lý và hỗ trợ những bài bác tập dượt thực hành thực tế nhằm các bạn tập luyện khả năng thực tiễn.\"
MÔN TOÁN - LỚP 8 | KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG | 10H00 NGÀY 31.03.2020
\"Gặp trở ngại vô môn Toán? Video này là mối cung cấp tư liệu học tập phụ cho tới học viên môn Toán. Nắm vững vàng những kỹ năng và kiến thức căn bạn dạng và học tập cơ hội giải những bài bác tập dượt một cơ hội hiệu suất cao.\"
Tính hóa học và phần mềm của nhị tam giác đồng dạng vô đánh giá học?
Hai tam giác được gọi là đồng dạng nếu như đem những góc tương đương và tỉ trọng giống hệt Một trong những cạnh của bọn chúng. Tính hóa học cần thiết của nhị tam giác đồng dạng vô đánh giá học tập là:
1. Tính hóa học tỉ lệ: Khi nhị tam giác đồng dạng, tỷ trọng giống hệt Một trong những cạnh của bọn chúng. Vấn đề này tức là toàn bộ những cạnh của tam giác gốc hoàn toàn có thể nhân hoặc phân tách đôi khi cho 1 hằng số nhằm nhận được cạnh ứng của tam giác đồng dạng.
2. Tính hóa học góc tương đồng: Khi nhị tam giác đồng dạng, góc ứng của bọn chúng cũng tương đương. Vấn đề này tức là những góc vô tam giác gốc hoàn toàn có thể tương đương với những góc ứng vô tam giác đồng dạng.
3. Tính hóa học tỷ trọng diện tích S: Diện tích của nhị tam giác đồng dạng tỉ trọng bình phương với tỷ số thân ái phỏng lâu năm những cạnh ứng của bọn chúng. Vấn đề này tức là nếu như tỷ số phỏng lâu năm những cạnh ứng của nhị tam giác đồng dạng là a/b, thì tỷ số diện tích S của bọn chúng là a^2/b^2.
Ứng dụng của nhị tam giác đồng dạng vô đánh giá học tập thật nhiều, bao gồm:
1. Giải quyết Việc đo lường và tính toán và vẽ hình: Khi biết những mối quan hệ đồng dạng thân ái nhị tam giác, tất cả chúng ta hoàn toàn có thể đo lường những độ cao thấp ko biết của những tam giác, hoặc khởi tạo lại hình dạng của một hình.
2. Thiết nối tiếp tế bào hình: Việc dùng đồng dạng vô design quy mô được cho phép tao đưa đến một quy mô đem độ cao thấp nhỏ rộng lớn hoặc to hơn bám theo tỷ trọng chắc chắn đối với quy mô gốc.
3. Ứng dụng vô công nghệ: Các nguyên tắc đồng dạng được dùng trong số nghành nghề như hình họa PC, phân tách hình hình họa, xử lý hình họa và technology 3 chiều.
Tóm lại, nhị tam giác đồng dạng đeo đặc thù cần thiết và phần mềm thoáng rộng vô đánh giá học tập, hùn tất cả chúng ta giải quyết và xử lý Việc đo lường và tính toán, vẽ hình, design quy mô và phần mềm vô technology.
_HOOK_
Mối mối quan hệ thân ái nhị tam giác đồng dạng và tỉ số tỷ lệ?
Mối mối quan hệ thân ái nhị tam giác đồng dạng và tỉ số tỷ trọng là cực kỳ cần thiết vô nghành nghề hình học tập. Khi nhị tam giác đồng dạng, tỉ số những cạnh ứng của bọn chúng tiếp tục đều bằng nhau. Vấn đề này tức là những đàng cao, những đàng trung tuyến, những đàng phân giác, và những đàng viền của nhị tam giác cũng tiếp tục tạo ra trở thành những đàng tương tự động.
Để xác lập coi nhị tam giác đem đồng dạng hay là không, tất cả chúng ta cần thiết đối chiếu cả những góc và những cạnh ứng của bọn chúng. Thông qua loa đối chiếu những góc, tất cả chúng ta hoàn toàn có thể vận dụng những quy tắc của tam giác đồng dạng như góc đồng đẳng và góc phân giác nhằm xác lập tính đồng dạng của bọn chúng.
Sau Lúc xác lập nhị tam giác đồng dạng, tất cả chúng ta hoàn toàn có thể dùng tỉ số tỷ trọng nhằm màn biểu diễn quan hệ Một trong những cạnh ứng của bọn chúng. Tỉ số tỷ trọng được xem bằng phương pháp phân tách phỏng lâu năm của những cạnh ứng, ví như tỉ số Một trong những cạnh đối lập với gốc ứng.
Tỉ số tỷ trọng này là một số trong những hữu tỷ và ko thay đổi cho tới toàn bộ những cạnh ứng của nhị tam giác đồng dạng. Nó được cho phép tất cả chúng ta màn biểu diễn quan hệ về độ cao thấp Một trong những đối tượng người dùng hình học tập không giống nhau.
Ví dụ, nếu như tỉ số tỷ trọng thân ái nhị cạnh của nhị tam giác đồng dạng là 2:3, điều này tức là cạnh của tam giác loại nhị dài ra hơn nữa 1.5 lượt đối với cạnh ứng của tam giác loại nhất.
Từ cơ, tao hoàn toàn có thể sử dụng tỉ số tỷ trọng nhằm đo lường những độ cao thấp của những đối tượng người dùng hình học tập trong số Việc tương quan cho tới nhị tam giác đồng dạng.
Trường hợp ý quan trọng Lúc nhị tam giác đồng dạng đeo những góc và cạnh vày nhau?
Trường hợp ý quan trọng Lúc nhị tam giác đồng dạng đeo những góc và cạnh đều bằng nhau được gọi là tam giác giống hệt. Vấn đề này tức là nhị tam giác đem nằm trong đỉnh và những cạnh ứng của bọn chúng đều đồng đều bằng nhau. Trong tình huống này, tỉ trọng thân ái độ cao thấp nhị tam giác là 1:1.
Để minh chứng sự giống hệt của nhị tam giác, tao cần thiết tuân theo công việc sau:
Bước 1: Xác quyết định nhị tam giác cần thiết minh chứng giống hệt.
Bước 2: Kiểm tra coi những cạnh và những góc ứng của nhị tam giác đem đều bằng nhau ko.
Bước 3: Nếu những cạnh và những góc ứng của nhị tam giác đều bằng nhau, tao Kết luận rằng nhị tam giác giống hệt.
Ví dụ, nếu như đem nhị tam giác ABC và A\'B\'C\', vô cơ AB = A\'B\', AC = A\'C\' và BC = B\'C\', và những góc ứng của nhị tam giác đều đều bằng nhau (như góc A = góc A\', góc B = góc B\' và góc C = góc C\'), tao hoàn toàn có thể Kết luận rằng nhị tam giác giống hệt.
Lưu ý rằng, việc những cạnh và những góc ứng của nhị tam giác đều bằng nhau đơn thuần ĐK đầy đủ nhằm nhị tam giác được xem là giống hệt. Để chắc chắn là, tao cần thiết xác lập thêm thắt ĐK quan trọng không giống, ví dụ điển hình như các góc không giống đều bằng nhau hoặc tỉ trọng giống hệt của những cạnh.
Toán học tập 8 - Bài 4 - Khái niệm nhị tam giác đồng dạng - Cô Nguyễn Thị Ngọc Ánh
\"Bạn ham muốn học tập Toán và một nghề giáo giỏi? Hãy coi đoạn Clip của Cô Nguyễn Thị Ngọc Ánh. Cô ấy tiếp tục khiến cho bạn nắm rõ những định nghĩa khó khăn và lý giải một cơ hội dễ nắm bắt.\"
Cách minh chứng nhị tam giác đồng dạng dựa vào những ĐK vẫn cho?
Cách minh chứng nhị tam giác đồng dạng dựa vào những ĐK vẫn cho tới như sau:
1. Vế tam giác: Trước tiên, tao cần thiết chắc chắn là rằng nhị tam giác cần thiết minh chứng đồng dạng đeo nằm trong nhị cặp góc tương tự. Vấn đề này hoàn toàn có thể được minh chứng bằng phương pháp dùng những quyết định lý về góc (ví dụ như góc nội tiếp, góc nước ngoài tiếp, góc ví le...).
2. Cạnh tam giác: Tiếp bám theo, tao cần thiết đánh giá coi tỉ trọng thân ái phỏng lâu năm những cạnh của nhị tam giác đem đều bằng nhau hay là không. Để thực hiện điều này, tao hoàn toàn có thể dùng những công thức hoặc quy tắc như quyết định lý đồng tỉ trọng hoặc quy tắc xác xác định trí vô tam giác.
3. Kết luận: Sau Lúc vẫn xác lập được nhị tam giác đem nằm trong nhị cặp góc tương tự và tỉ trọng cạnh thân ái bọn chúng đều bằng nhau, tao hoàn toàn có thể Kết luận rằng nhị tam giác cơ đồng dạng.
Việc minh chứng đồng dạng của nhị tam giác dựa vào những ĐK vẫn cho tới này hoàn toàn có thể đòi hỏi kỹ năng và kiến thức và khả năng rõ ràng về hình học tập và toán học tập. Dựa vô Việc rõ ràng và những ĐK vẫn cho tới, tao hoàn toàn có thể vận dụng những luật lệ chuyển đổi và những công thức vô hình học tập nhằm minh chứng đồng dạng của nhị tam giác.
Các luật lệ chuyển đổi nhằm minh chứng nhị tam giác đồng dạng?
Để minh chứng nhị tam giác đồng dạng, tất cả chúng ta hoàn toàn có thể dùng những luật lệ chuyển đổi sau:
1. Phép chuyển đổi tương tự:
- Tương tự động thân ái nhị tam giác xẩy ra Lúc tỉ trọng những cạnh ứng của bọn chúng đều bằng nhau.
- Để minh chứng đồng dạng thân ái nhị tam giác, tao hoàn toàn có thể đối chiếu tỉ trọng Một trong những cạnh ứng của bọn chúng.
2. Phép chuyển đổi hạn chế và nhân đôi:
- Chúng tao hoàn toàn có thể hạn chế một tam giác và tiếp sau đó nhân song độ cao thấp của chính nó muốn tạo rời khỏi một tam giác đem đồng dạng với tam giác thuở đầu.
3. Phép chuyển đổi bám theo góc:
- Các tam giác đồng dạng nhau Lúc mang 1 góc Một trong những cạnh ứng đều bằng nhau.
- Chúng tao hoàn toàn có thể minh chứng đồng dạng thân ái nhị tam giác bằng phương pháp đối chiếu những góc ứng của bọn chúng.
4. Phép chuyển đổi bám theo tỉ số diện tích:
- Hai tam giác đồng dạng nhau Lúc tỉ số diện tích S của bọn chúng đều bằng nhau.
- Để minh chứng đồng dạng, tao hoàn toàn có thể tính diện tích S của những tam giác và đối chiếu tỉ số diện tích S của bọn chúng.
Chúng tao hoàn toàn có thể vận dụng một hoặc nhiều luật lệ chuyển đổi bên trên nhằm minh chứng đồng dạng thân ái nhị tam giác.
Xem thêm: nhất chí hay nhất trí
Bài toán đề ra kể từ định nghĩa nhị tam giác đồng dạng và cơ hội giải quyết?
Ðể giải Việc tương quan cho tới định nghĩa nhị tam giác đồng dạng, tao tiến hành công việc sau:
Bước 1: Đọc và hiểu đề bài
Đầu tiên, hiểu kỹ đề bài bác và hiểu đòi hỏi của chính nó. Xem xét vấn đề hỗ trợ vô đề bài bác, như các Điểm sáng của nhị tam giác đang rất được nói đến và những vấn đề không giống hoàn toàn có thể tương quan cho tới Việc.
Bước 2: Xác quyết định những vấn đề cần triệu chứng minh
Dựa bên trên đề bài bác, kiểm tra những đòi hỏi cần thiết minh chứng. Vấn đề này hoàn toàn có thể bao hàm việc minh chứng nhị tam giác đồng dạng, xác lập những thông số tỷ trọng Một trong những cạnh của nhị tam giác, hoặc mò mẫm một địa điểm rõ ràng vô tam giác đồng dạng.
Bước 3: sít dụng những quy tắc, khái niệm và công thức
Dựa vô kỹ năng và kiến thức về tam giác và nhị tam giác đồng dạng, vận dụng những quy tắc, khái niệm và công thức nhằm giải quyết và xử lý Việc. Đồng thời, người giải cần dùng lý thuyết và dụng cụ tương thích để mang rời khỏi được câu vấn đáp đích thị.
Bước 4: Tạo một dàn ý hoặc sơ loại nhằm giải bài bác toán
Trước Lúc chính thức giải Việc, tạo ra một dàn ý hoặc sơ loại nhằm trình diễn công việc giải quyết và xử lý. Vấn đề này sẽ hỗ trợ người giải đưa đến một plan rõ nét và giới hạn sơ sót vô quy trình giải.
Bước 5: Thực hiện tại công việc giải quyết
Tiến hành tiến hành công việc giải quyết và xử lý bám theo dàn ý hoặc sơ loại vẫn tạo ra. Trong quy trình này, người giải cần thiết để ý cho tới việc dùng đúng mực những công thức, hình học tập và logic nhằm giải quyết và xử lý Việc đích thị.
Bước 6: Kiểm tra lại và trình diễn kết quả
Sau Lúc hoàn thiện việc giải quyết và xử lý Việc, cần thiết ra soát thành phẩm nhằm đáp ứng tính đúng mực. Nếu cần thiết, hoàn toàn có thể trình diễn thành phẩm bám theo đòi hỏi của đề bài bác hoặc lý giải phương pháp giải quyết và xử lý của tôi.
Tuy nhiên, tùy nằm trong vô Việc rõ ràng, công việc giải quyết và xử lý hoàn toàn có thể đem sự không giống nhau. Việc nắm rõ lý thuyết và phần mềm những công thức, quy tắc và khái niệm tương quan cho tới nhị tam giác đồng dạng là cực kỳ cần thiết nhằm giải quyết và xử lý Việc thành công xuất sắc.

_HOOK_












Bình luận