Chủ đề xác lập tâm đường tròn nội tiếp tam giác: Xác quyết định tâm đường tròn nội tiếp tam giác là một trong tiến độ cần thiết vô hình học tập tam giác. bằng phẳng cơ hội dò thám gửi gắm điểm của 3 đàng phân giác của tam giác, tất cả chúng ta rất có thể xác xác định trí đúng mực của tâm đàng tròn trĩnh nội tiếp. Vấn đề này gom tất cả chúng ta nắm rõ rộng lớn về cấu hình của tam giác và vận dụng vô những Việc không giống nhau vô học hành và thực dẫn.
Làm sao nhằm xác lập tâm đường tròn nội tiếp tam giác?
Để xác lập tâm đường tròn nội tiếp tam giác, tất cả chúng ta rất có thể dùng nhị cách thức không giống nhau:
1. Sử dụng đàng trung trực:
- Vẽ những đàng trung trực của những cạnh tam giác.
- Đường trung trực của nhị cạnh sẽ sở hữu được nút giao nhau là tâm đường tròn nội tiếp tam giác.
- Sử dụng thước nhằm đo khoảng cách kể từ tâm cho tới phụ thân đỉnh tam giác nhằm xác lập nửa đường kính đàng tròn trĩnh nội tiếp.
2. Sử dụng đàng phân giác:
- Vẽ những đàng phân giác của những góc tam giác.
- Đường phân giác của nhị góc sẽ sở hữu được nút giao nhau là tâm đường tròn nội tiếp tam giác.
- Sử dụng thước nhằm đo khoảng cách kể từ tâm cho tới phụ thân đỉnh tam giác nhằm xác lập nửa đường kính đàng tròn trĩnh nội tiếp.
Với cả nhị cách thức bên trên, tất cả chúng ta cần dùng thước nhằm đo khoảng cách kể từ tâm cho tới phụ thân đỉnh tam giác, kể từ cơ xác lập được nửa đường kính đàng tròn trĩnh nội tiếp. Sau cơ, rất có thể vẽ đàng tròn trĩnh nội tiếp tam giác bằng phương pháp người sử dụng cây viết và compa/bút chỉ nhằm mãi ở địa điểm vẽ được đàng tròn trĩnh ứng với nửa đường kính vẫn xác lập.
Lưu ý rằng, Khi tam giác là một trong tam giác vuông, đàng tròn trĩnh nội tiếp cũng chính là đàng tròn trĩnh nước ngoài tiếp của tam giác. Trong tình huống này, tâm đàng tròn trĩnh nội tiếp tiếp tục trùng với đỉnh góc vuông của tam giác.
Thông qua quýt những cách thức bên trên, tất cả chúng ta rất có thể xác lập tâm đường tròn nội tiếp tam giác một cơ hội đơn giản dễ dàng và đúng mực.
Bạn đang xem: tâm đường tròn nội tiếp tam giác

Tại sao từng một tam giác chỉ mất có một không hai 1 đàng tròn trĩnh nội tiếp?
Mỗi một tam giác chỉ mất có một không hai một đàng tròn trĩnh nội tiếp vì thế đấy là một đặc điểm đặc thù của tam giác. Đường tròn trĩnh nội tiếp tam giác đó là đàng tròn trĩnh trải qua cả phụ thân đỉnh của tam giác và đem tâm phía trên gửi gắm điểm của phụ thân đàng phân giác của tam giác.
Để nắm rõ rộng lớn về đặc điểm này, tất cả chúng ta rất có thể kiểm tra từng bước sau đây:
Bước 1: Tam giác ABC đem phụ thân đỉnh A, B và C.
Bước 2: Đường tròn trĩnh nội tiếp tam giác là một trong đàng tròn trĩnh tuy nhiên điểm tâm của chính nó phía trên gửi gắm điểm của phụ thân đàng phân giác của tam giác. Gọi I là tâm đường tròn nội tiếp tam giác ABC.
Bước 3: Ta hiểu được từng đàng phân giác của tam giác là đường thẳng liền mạch trải qua đỉnh của tam giác và phân tách song góc ứng của tam giác. Vì vậy, gửi gắm điểm của phụ thân đàng phân giác là vấn đề I sao cho tới kể từ I cho tới A, I cho tới B và I cho tới C đem nằm trong khoảng cách.
Bước 4: Do tam giác đem chính phụ thân đỉnh, và từng đỉnh được nối với trung điểm của cạnh đối lập vì thế một đường thẳng liền mạch, nên đường thẳng liền mạch này được xem là đàng phân giác và trải qua tâm đường tròn nội tiếp tam giác.
Bước 5: Với fake sử ngược lại rằng đem hai tuyến đường tròn trĩnh nội tiếp tam giác, tao rất có thể chứng tỏ rằng nhị tâm đàng tròn trĩnh nội tiếp này nằm trong trùng cùng nhau. Do cơ, từng tam giác chỉ mất có một không hai một đàng tròn trĩnh nội tiếp.
Trên đấy là nguyên nhân chủ yếu tại vì sao từng một tam giác chỉ mất có một không hai một đàng tròn trĩnh nội tiếp trải qua phụ thân đỉnh của chính nó.
Làm thế này nhằm xác lập tâm của đàng tròn trĩnh nội tiếp tam giác?
Để xác lập tâm của đàng tròn trĩnh nội tiếp tam giác, tất cả chúng ta rất có thể vận dụng một trong những cách thức sau:
1. Sử dụng gửi gắm điểm của những đàng phân giác: Đường phân giác của một tam giác là đường thẳng liền mạch trải qua đỉnh tam giác và phân tách góc bên trên đỉnh cơ trở thành nhị góc đều nhau. bằng phẳng kiểu vẽ đàng phân giác cho tới từng cặp góc của tam giác, tao sẽ sở hữu được phụ thân đàng phân giác. Tâm của đàng tròn trĩnh nội tiếp tam giác được xem là gửi gắm điểm của phụ thân đàng phân giác này.
2. Sử dụng trung tuyến: Trung tuyến của một tam giác là đường thẳng liền mạch nối trung điểm của nhị đỉnh ngẫu nhiên của tam giác với đỉnh sót lại. Ta rất có thể vẽ trung tuyến cho từng cặp đỉnh của tam giác và dò thám nút giao nhau của những trung tuyến này. Điểm cơ đó là tâm của đàng tròn trĩnh nội tiếp tam giác.
3. Sử dụng hình học tập vector: bằng phẳng cơ hội dùng hình học tập vector và những công thức tương quan, tao rất có thể đo lường được tọa chừng của tâm đàng tròn trĩnh nội tiếp. Một cơ hội thông thườn là dùng công thức sau: Tâm đàng tròn trĩnh nội tiếp tam giác ABC đem tọa chừng (x, y) với x = \\(\\frac{{a \\cdot x_A + b \\cdot x_B + c \\cdot x_C}}{{a + b + c}}\\) và nó = \\(\\frac{{a \\cdot y_A + b \\cdot y_B + c \\cdot y_C}}{{a + b + c}}\\), vô cơ (x_A, y_A), (x_B, y_B), (x_C, y_C) là tọa chừng của phụ thân đỉnh của tam giác ABC và a, b, c theo lần lượt là chừng lâu năm những cạnh ứng.
Tùy nằm trong vô Việc rõ ràng, tao rất có thể vận dụng một trong số cách thức bên trên nhằm xác lập tâm của đàng tròn trĩnh nội tiếp tam giác.
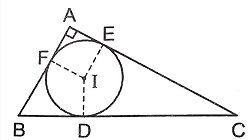
Có cơ hội này không giống nhằm xác lập tâm đường tròn nội tiếp tam giác không?
Có rất nhiều cách thức không giống nhau nhằm xác lập tâm đường tròn nội tiếp tam giác. Dưới đấy là một vài ba cơ hội phổ biến:
1. Cách 1: Sử dụng gửi gắm điểm của những đàng trung trực của những cạnh tam giác.
- Vẽ những đàng trung trực của những cạnh của tam giác.
- Đường trung trực của một cạnh đó là đường thẳng liền mạch trải qua đằm thắm điểm ở chính giữa cạnh cơ và đỉnh ứng.
- Giao điểm của những đàng trung trực đó là tâm của đàng tròn trĩnh nội tiếp tam giác.
2. Cách 2: Sử dụng gửi gắm điểm của những đàng phân giác của những góc tam giác.
- Vẽ những đàng phân giác của những góc vô tam giác.
- Đường phân giác của một góc đó là đường thẳng liền mạch phân tách góc cơ trở thành nhị phần đều nhau.
- Giao điểm của những đàng phân giác đó là tâm của đàng tròn trĩnh nội tiếp tam giác.
3. Cách 3: Sử dụng điểm Fermat của tam giác.
- Điểm Fermat của tam giác đó là điểm vô tam giác tuy nhiên tổng khoảng cách kể từ điểm cơ cho tới những đỉnh tam giác là nhỏ nhất.
- Để xác lập điểm Fermat, tao rất có thể dùng quy tắc vẽ hình giản vô tam giác đều.
- Giao điểm của những đường thẳng liền mạch trải qua những đỉnh tam giác tới điểm Fermat đó là tâm của đàng tròn trĩnh nội tiếp tam giác.
Tuy đem rất nhiều cách thức không giống nhau nhằm xác lập tâm đường tròn nội tiếp tam giác, tuy nhiên cả phụ thân cơ hội bên trên đều đáp ứng tìm kiếm được tâm của đàng tròn trĩnh nội tiếp tam giác.
Xác quyết định tọa chừng tâm đường tròn nội tiếp tam giác ABC
\"Hãy tìm hiểu tọa chừng tâm đường tròn nội tiếp tam giác trải qua Clip chỉ dẫn thú vị này! quý khách hàng tiếp tục nắm rõ về kiểu cách dò thám tọa chừng tâm, đôi khi vận dụng hoạt bát vô những Việc thực tiễn. Đừng bỏ qua nhé!\"
Bấm PC thời gian nhanh tâm đường tròn nội tiếp tam giác vô không khí Oxyz - Thầy Nguyễn Phan Tiến
\"Bạn ham muốn phát triển thành một Chuyên Viên bấm PC nhanh? Video chỉ dẫn này sẽ hỗ trợ bạn! Từ những mẹo và thủ pháp đơn giản và giản dị cho tới kĩ năng vàng, các bạn sẽ nhanh gọn lẹ nâng cao vận tốc và hiệu suất. Hãy truy vấn ngay!\"
Cách này nhằm vẽ đàng tròn trĩnh nội tiếp tam giác?
Để vẽ được đàng tròn trĩnh nội tiếp tam giác, tao cần thiết xác lập tâm và nửa đường kính của đàng tròn trĩnh. Dưới đấy là phương pháp để thực hiện điều này:
Bước 1: Vẽ tam giác ABC với những đỉnh A, B, và C được biết trước.
Bước 2: Xác quyết định đàng phân giác của những góc vô tam giác. Để thực hiện điều này, vẽ những đàng phân giác kể từ từng đỉnh cho tới mặt mũi phẳng phiu đối lập.
Bước 3: Tìm gửi gắm điểm của những đàng phân giác. Điểm gửi gắm điểm đó là tâm của đàng tròn trĩnh nội tiếp tam giác.
Bước 4: Đo chừng lâu năm kể từ tâm cho tới một trong các phụ thân đỉnh của tam giác. Đây đó là nửa đường kính của đàng tròn trĩnh nội tiếp tam giác.
Bước 5: Sử dụng tâm và nửa đường kính vẫn xác lập nhằm vẽ đàng tròn trĩnh nội tiếp tam giác.
Lưu ý rằng bên dưới đấy là hướng dẫn cơ phiên bản nhằm vẽ đàng tròn trĩnh nội tiếp tam giác. Việc xác lập tâm và nửa đường kính rất có thể không giống nhau tùy nằm trong vô những vấn đề vẫn biết về tam giác.
Xem thêm: nam trung bộ gồm những tỉnh nào
_HOOK_
Làm thế này nhằm xác lập những đàng phân giác của tam giác?
Để xác lập những đàng phân giác của tam giác, tất cả chúng ta rất có thể tuân theo công việc sau:
Bước 1: Lấy tam giác ABC đem những đỉnh là A, B, C.
Bước 2: Vẽ nhị đoạn trực tiếp kể từ đỉnh A trải qua trung điểm của cạnh BC, và kể từ đỉnh B trải qua trung điểm của cạnh AC. Gọi nhị nút giao nhau của nhị đoạn trực tiếp này là D và E.
Bước 3: Kết nối điểm D với đỉnh C và điểm E với đỉnh C.
Kết ngược, tao sẽ sở hữu được phụ thân đàng phân giác của tam giác ABC là đàng phân giác góc A, đàng phân giác góc B và đàng phân giác góc C, với ứng là AD, BE và CF.
Công thức này dùng làm tính tọa chừng tâm đường tròn nội tiếp tam giác?
Công thức được dùng nhằm tính tọa chừng tâm đường tròn nội tiếp tam giác là gửi gắm điểm của 3 đàng phân giác của tam giác. quý khách hàng rất có thể vận dụng công việc sau nhằm tính tọa chừng tâm đường tròn nội tiếp tam giác:
Bước 1: Xác quyết định những đỉnh của tam giác.
Đầu tiên, bạn phải xác lập tọa chừng của những đỉnh A, B và C của tam giác.
Bước 2: Tính toán đàng phân giác.
Tiếp theo gót, chúng ta đo lường đàng phân giác cho tới từng cạnh của tam giác. Đường phân giác của một cạnh được xem bằng phương pháp lấy 50% chừng lâu năm của cạnh và kết phù hợp với đường thẳng liền mạch nối đỉnh gốc của cạnh với tâm cạnh cơ.
Bước 3: Tìm gửi gắm điểm của đàng phân giác.
Sau Khi đo lường được những đàng phân giác cho tới từng cạnh của tam giác, bạn phải dò thám nút giao của phụ thân đàng phân giác. Điểm này đó là tọa chừng của tâm đường tròn nội tiếp tam giác.
Với công việc bên trên, chúng ta cũng có thể xác lập tọa chừng của tâm đường tròn nội tiếp tam giác.
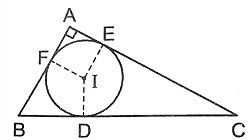
Cách vẽ đàng tròn trĩnh nội tiếp tam giác đơn giản và giản dị dễ nắm bắt - Toán lớp 9
\"Đường tròn trĩnh nội tiếp tam giác rất có thể đẹp mắt và hợp lý và phải chăng như vậy nào? Xem Clip này nhằm biết phương pháp vẽ đàng tròn trĩnh nội tiếp tam giác một cơ hội dễ dàng dàng! quý khách hàng tiếp tục tìm hiểu cơ hội dùng công thức và đàng kẻ để sở hữu thành phẩm trả hảo!\"
Bán kính đàng tròn trĩnh nội tiếp tam giác được xem như vậy nào?
Để tính nửa đường kính đàng tròn trĩnh nội tiếp tam giác, tao rất có thể thực hiện như sau:
Bước 1: Tìm tọa chừng những đỉnh của tam giác. Gọi A(xA, yA), B(xB, yB), C(xC, yC) là tọa chừng của phụ thân đỉnh tam giác.
Bước 2: Tìm chừng lâu năm những cạnh tam giác. Sử dụng công thức khoảng cách đằm thắm nhị điểm vô mặt mũi phẳng phiu nhằm tính chừng lâu năm cạnh AB, BC và AC.
Bước 3: Tính diện tích S tam giác. Sử dụng công thức diện tích S tam giác Heron nhằm tính diện tích S S của tam giác đem cạnh AB, BC và AC. Công thức này là:
S = sqrt(p * (p - AB) * (p - BC) * (p - AC))
Trong cơ, p = (AB + BC + AC) / 2 là nửa chu vi tam giác.
Bước 4: Tính nửa đường kính đàng tròn trĩnh nội tiếp tam giác. Bán kính R của đàng tròn trĩnh nội tiếp tam giác rất có thể được xem vì thế công thức sau:
R = S / p
Bước 5: Xác quyết định tâm đàng tròn trĩnh nội tiếp. Tìm tọa chừng của tâm đàng tròn trĩnh nội tiếp I(xI, yI) bằng phương pháp tính trung điểm của những đỉnh tam giác. Tức là:
xI = (xA + xB + xC) / 3
yI = (yA + yB + yC) / 3
Như vậy, trải qua công việc bên trên, tao rất có thể tính được nửa đường kính và tọa chừng của tâm đường tròn nội tiếp tam giác.
Tại sao xác lập tâm đường tròn nội tiếp tam giác là một trong bước cần thiết vô xác lập những tính chất không giống của tam giác?
Xác quyết định tâm của đàng tròn trĩnh nội tiếp tam giác là một trong bước cần thiết trong các việc xác lập những tính chất không giống của tam giác vì thế như thế tất cả chúng ta rất có thể đơn giản dễ dàng đo lường và vận dụng những công thức và quy tắc tương quan cho tới đàng tròn trĩnh nội tiếp vô những Việc tam giác.
Khi tất cả chúng ta hiểu rằng tâm đường tròn nội tiếp tam giác, đặc điểm đó là vấn đề bên trên từng đàng phân giác và cơ hội đàng phân giác vẽ qua quýt tâm kể từ tam giác. Từ cơ, tất cả chúng ta rất có thể thấy rằng tam giác này còn có Đặc điểm là những đàng phân giác trải qua và một điểm, tức là tâm đàng tròn trĩnh nội tiếp.
Bằng cơ hội hiểu rằng tâm đàng tròn trĩnh nội tiếp, tất cả chúng ta rất có thể tính được nửa đường kính của đàng tròn trĩnh này. Bán kính vì thế 50% chừng lâu năm một cạnh tam giác này cơ. Vấn đề này đặc biệt hữu ích trong các việc đo lường những tính chất không giống của tam giác như diện tích S, chu vi và những góc của tam giác.
Ngoài đi ra, xác lập tâm đàng tròn trĩnh nội tiếp cũng gom tất cả chúng ta nắm rõ rộng lớn về việc đối sánh tương quan trong những thành phần vô tam giác. Từ cơ, tất cả chúng ta rất có thể vận dụng những quy tắc và công thức tương quan cho tới đàng tròn trĩnh nội tiếp vô những Việc tam giác khác ví như chứng tỏ đẳng giác, đẳng cạnh và đẳng đỉnh.
Điều cần thiết là xác lập tâm đường tròn nội tiếp tam giác gom tất cả chúng ta dò thám hiểu và phân tách tam giác một cơ hội cụ thể và rõ rệt, kể từ cơ gom tất cả chúng ta xử lý những Việc tương quan cho tới tam giác một cơ hội đơn giản dễ dàng và đúng mực rộng lớn.
Xem thêm: hoàn cảnh sáng tác chuyện người con gái nam xương
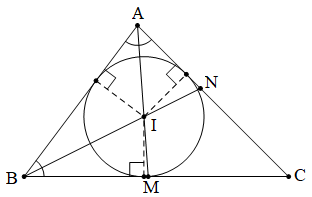
Có đặc điểm này đặc biệt quan trọng hoặc cần thiết về tâm đường tròn nội tiếp tam giác tuy nhiên tất cả chúng ta cần phải biết không?
Có một trong những đặc điểm cần thiết về tâm đường tròn nội tiếp tam giác tuy nhiên tất cả chúng ta cần thiết biết:
1. Tâm đàng tròn trĩnh nội tiếp tam giác phía trên đàng phân giác của những góc vô tam giác: Tâm đàng tròn trĩnh nội tiếp tam giác là vấn đề trùng nhau của phụ thân đàng phân giác góc vô tam giác. Vấn đề này Có nghĩa là tâm đường tròn nội tiếp tam giác được xác lập bằng phương pháp gửi gắm điểm của những đàng phân giác góc vô.
2. Tâm đàng tròn trĩnh nội tiếp là trung điểm của những đàng cao: Đường cao của một tam giác là đường thẳng liền mạch trải qua một đỉnh của tam giác và vuông góc với cạnh đối lập. Tâm đàng tròn trĩnh nội tiếp tam giác phía trên những đàng cao và là trung điểm của bọn chúng.
3. Tâm đàng tròn trĩnh nội tiếp bao gồm những đoạn trực tiếp vuông góc: Tâm đàng tròn trĩnh nội tiếp tam giác phía trên những đoạn trực tiếp vuông góc kể từ những đỉnh của tam giác cho tới những đỉnh của tam giác đối lập. Vấn đề này Có nghĩa là tâm đàng tròn trĩnh nội tiếp là tâm của đàng trục của tam giác.
4. Bán kính đàng tròn trĩnh nội tiếp tam giác: Bán kính đàng tròn trĩnh nội tiếp tam giác được xem vì thế nửa chu vi của tam giác phân tách cho tới diện tích S tam giác. Bán kính này cũng đó là khoảng cách kể từ tâm đàng tròn trĩnh nội tiếp cho tới ngẫu nhiên đỉnh này của tam giác.
Những đặc điểm bên trên đặc biệt cần thiết trong các việc xử lý những Việc tương quan cho tới tam giác và đàng tròn trĩnh nội tiếp.
_HOOK_












Bình luận