Bách khoa toàn thư há Wikipedia
Bài này ghi chép về đơn vị chức năng đo góc. Đối với đơn vị chức năng đo liều mạng lượng sự phản xạ, coi Rad (đơn vị). Đối với những khái niệm không giống, coi Radian (định hướng).
Bạn đang xem: đổi từ độ sang rad
| Radian | |
|---|---|
| Hệ thống đơn vị | Đơn vị dẫn xuất SI |
| Đơn vị của | Góc |
| Kí hiệu | rad hoặc c |
| Chuyển thay đổi đơn vị | |
| 1 rad nhập ... | ... vị ... |
| milliradian | 1,000 milliradian |
| turn | 1/2π turn |
| độ | 180/π ≈ 57.296° |
| gon | 200/π ≈ 63.662g |
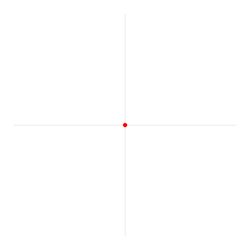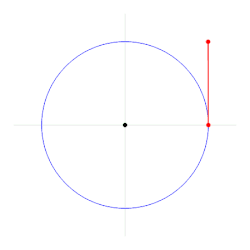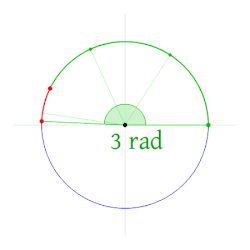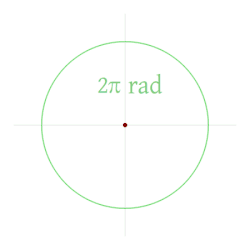
Radian (có thể phát âm là ra-đi-an) là 1 trong những đơn vị chức năng chuẩn chỉnh đo góc bằng và được sử dụng thịnh hành nhập toán học tập. Radian là 1 trong những đơn vị chức năng tỷ trọng tựa như Decibel, Tức là nó không tồn tại đại lượng song lập ví dụ, nó là tỷ trọng phỏng nhiều năm cung tròn xoe bên trên phỏng nhiều năm nửa đường kính. Vì thế, 1 rad ứng với nửa đường kính 5m là cung tròn xoe 5m. Trong vẽ nghệ thuật, khi cần thiết vẽ một cung tròn xoe phỏng nhiều năm chắc chắn, người vẽ cần được tiến hành thông số kỹ thuật nửa đường kính (có đơn vị chức năng setup trước hoặc đơn vị chức năng rỗng) và đơn vị chức năng góc radian. Đối với đàng tròn xoe đơn vị chức năng, kích cỡ góc radian vị luôn luôn chiều nhiều năm cung tròn xoe, nhưng mà chu vi nửa cung tròn xoe là , tương tự vì vậy 1 radian bằng phỏng (xấp xỉ 57,3 độ), với đàng tròn xoe không giống đàng tròn xoe đơn vị chức năng, 1 radian đạt được khi chiều nhiều năm cung tròn xoe vị với nửa đường kính đàng tròn xoe. Radian vốn liếng dĩ từng là đơn vị chức năng bổ sung cập nhật SI vì thế theo dõi khái niệm , bởi vậy nó không tồn tại đơn vị chức năng là chính vì vậy. Nhưng cũng chính vì quan hệ tỷ trọng trực tiếp của chính nó với đơn vị chức năng đo góc nhìn nên nó được gọi là là radian và được sử dụng thay cho thế mang đến đơn vị chức năng đo góc độ; tuy vậy, phân mục đơn vị chức năng này bị quăng quật từ thời điểm năm 1995 và kể từ cơ radian sẽ là đơn vị chức năng dẫn xuất SI. Đơn vị SI nhằm đo góc khối là steradian.
Radian được ký hiệu là rad hoặc khan hiếm rộng lớn là chữ c ghi chép lên bên trên (c). Ví dụ, 1 radian được ký hiệu là một trong những rad hoặc 1 c (thường bị thiếu sót trở nên "1°").
Định nghĩa[sửa | sửa mã nguồn]

Một radian là phỏng đo góc bằng thân thiết nhì nửa đường kính của một đàng tròn xoe rời bên trên một vòng tròn xoe với cung với chiều nhiều năm vị nửa đường kính.[1] Tổng quát lác rộng lớn, kích cỡ tính vị radian tương tự với tỉ số thân thiết chiều nhiều năm cung tròn xoe và nửa đường kính đàng tròn xoe. Công thức tính là θ = s /r, nhập cơ "θ" là góc chắn cung (tính vị radian), "s" là chiều nhiều năm cung còn "r" là nửa đường kính. trái lại, chiều nhiều năm cung bị khuất vị nửa đường kính đàng tròn xoe nhân với kích cỡ của góc chắn cung tính vị radian; công thức là s = rθ. Do là tỉ số thân thiết hai phía nhiều năm nên radian là độ quý hiếm ko loại nguyên vẹn, tức ko cần thiết ký hiệu đơn vị chức năng kèm theo, bởi vậy nhập toán học tập gần như là người tao ko ghi chép ký hiệu "rad". Trong tình huống không tồn tại ký hiệu đơn vị chức năng kèm theo thì nên hiểu độ quý hiếm đo góc cơ tính vị radian, trong những lúc nếu như độ quý hiếm cơ đo vị phỏng thì cần phải có ký hiệu °.
Độ rộng lớn tính vị radian của một vòng hoàn hảo (360 độ) là vị chiều nhiều năm chu vi phân tách mang đến nửa đường kính, tức là vị 2πr/r hoặc 2π.
Lịch sử[sửa | sửa mã nguồn]
Có mối cung cấp coi Roger Cotes là kẻ thể hiện định nghĩa radian nhập năm 1714.[2] Tuy nhiên, ý tưởng phát minh đo góc vị chiều nhiều năm cung tiếp tục với từ xưa cơ. Ghiyath al-Kashi (khoảng 1400) sử dụng "phần đàng kính" thực hiện đơn vị chức năng đo góc, nhập cơ 1 "phần đàng kính" tương tự 1/60 radian; ông cũng sử dụng những đơn vị chức năng nhỏ rộng lớn bằng phương pháp lấy những phần 2 lần bán kính phân tách mang đến 60.[3]
Thuật ngữ "radian" đợt trước tiên xuất hiện tại bên trên phiên bản in vào trong ngày 5 mon 6 năm 1873 vị James Thomson (anh của William Thomson) ở Trường Đại học tập Queen's, Belfast. Ông sử dụng kể từ này ngay lập tức từ thời điểm năm 1871, trong những lúc nhập năm 1869 thì Thomas Muir ở Đại học tập St. Andrews tiếp tục vì thế dự trong những kể từ "rad", "radial" và "radian". Năm 1874, Muir gật đầu sử dụng kể từ "radian" sau thời điểm tư vấn với James Thomson.[4][5][6]
Chuyển đổi[sửa | sửa mã nguồn]
Chuyển thay đổi thân thiết radian và độ[sửa | sửa mã nguồn]

Một radian tương tự 180/π phỏng. Do cơ khi mong muốn thay đổi kể từ radian quý phái phỏng thì lấy độ quý hiếm tính vị radian phân tách π nhân 180. trái lại, nhằm đổi từ độ sang radian thì lấy độ quý hiếm tính vị phỏng nhân với π/180.
Dẫn xuất của quy tắc quy đổi kể từ radian quý phái độ[sửa | sửa mã nguồn]
Chu vi đàng tròn xoe được xem vị công thức , nhập cơ là nửa đường kính đàng tròn xoe. Vì vậy với mối quan hệ tương tự sau:
[Do cần thiết con quay một góc nhằm vẽ được đàng tròn xoe trả chỉnh]
Theo khái niệm radian thì một đàng tròn xoe hoàn hảo thay mặt đại diện cho:
Kết thích hợp nhì quan hệ bên trên, thu được:
Chuyển thay đổi thân thiết radian và gradian[sửa | sửa mã nguồn]
radian tương tự 1 vòng, tức 400g. Vì vậy, nếu như muốn thay đổi kể từ radian quý phái gradian thì lấy độ quý hiếm tính vị radian nhân với ,. trái lại, nhằm thay đổi kể từ grad quý phái radian thì lấy độ quý hiếm tính vị grad nhân với
Bảng sau đây liệt kê những độ quý hiếm quy đổi hoặc dùng:
| Đơn vị | Giá trị | |||||||
|---|---|---|---|---|---|---|---|---|
| Vòng | 0 | 1 | ||||||
| Độ | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Radian | 0 | 2 | ||||||
| Gradian | 0g | 50g | 100g | 200g | 300g | 400g | ||
Thuận lợi của việc đo góc vị radian[sửa | sửa mã nguồn]

Trong vi tích phân và đa số những phân ngành của toán học tập - nước ngoài trừ hình học tập phần mềm - thì góc được đo thịnh hành vị radian. Vấn đề này là vì radian đem "bản hóa học tự động nhiên" của toán học tập, chung thể hiện tại nhiều sản phẩm cần thiết của toán học tập xinh xắn hơn.
Xem thêm: giải pháp bảo vệ môi trường
Các sản phẩm nhập giải tích toán học tập tương quan cho tới nồng độ giác coi tiếp tục gọn gàng và thích mắt khi được thể hiện tại vị radian. Ví dụ, việc sử dụng radian chung công thức số lượng giới hạn sau coi gọn gàng hơn:
Đây là gốc của không ít đẳng thức căn phiên bản nhập toán học tập, bao gồm
Do những đặc điểm này và những đặc điểm không giống nhưng mà những nồng độ giác sử dụng nhập lời nói giải những việc thông thường không tồn tại tương quan rõ nét với ý nghĩa sâu sắc hình học tập của hàm cơ (ví dụ lời nói giải của quy tắc vi phân , tính nguyên vẹn hàm ,...).
Các nồng độ giác cũng đều có mẫu mã gọn gàng và rất đẹp nếu như sử dụng đơn vị chức năng radian. Ví dụ chuỗi Taylor mang đến sin x:
Nếu "x" được thể hiện tại vị đơn vị chức năng phỏng thì chuỗi bên trên tiếp tục đựng được nhiều quá số rối rắm bên dưới dạng lũy quá của π/180:
Mối mối quan hệ thân thiết hàm sin và côsin và hàm nón (ví dụ, công thức Euler) cũng rất đẹp và gọn gàng rộng lớn với đơn vị chức năng là radian.
Phân tích loại nguyên[sửa | sửa mã nguồn]
Mặc cho dù radian là đơn vị chức năng đo lường và tính toán tuy nhiên nó là độ quý hiếm ko loại nguyên vẹn. cũng có thể thấy điều này kể từ khái niệm tiếp tục nêu: độ quý hiếm radian của góc ở tâm chắn cung tròn xoe vị với tỉ số thân thiết chiều nhiều năm cung bị khuất và nửa đường kính. Do đơn vị chức năng đo đã trở nên khử nhập sản phẩm nên tỉ số này là độ quý hiếm ko loại nguyên vẹn.
Mặc cho dù hệ tọa phỏng vô cùng và hệ tọa phỏng cầu sử dụng radian nhằm tế bào miêu tả tọa phỏng nhập không khí hai phía và tía chiều tuy nhiên radian là dẫn xuất kể từ tọa phỏng nửa đường kính, vì vậy số đo góc vị radian vẫn chính là ko loại nguyên vẹn.[7]
Dùng nhập cơ vật lý học[sửa | sửa mã nguồn]
Radian được dùng rộng thoải mái nhập cơ vật lý học tập khi cần thiết đo góc. Ví dụ, véc tơ vận tốc tức thời tầm nhìn công cộng được đo vị radian bên trên giây (rad/s). Một vòng xoay nhập một giây thì tương tự 2π rad/s.
Tương tự động, vận tốc góc cũng thông thường được đo vị radian bên trên giây bên trên giây (rad/s2).
Nhằm mục tiêu phân tách loại nguyên vẹn thì đơn vị chức năng ứng s−1 và s−2.
Pha của nhì sóng cũng đo vị radian. Ví dụ, nếu như phỏng lệch sóng thân thiết nhì sóng là (k·2π) radian (trong cơ k là số nguyên) thì bọn chúng sẽ là nằm trong trộn, trong những lúc nếu như phỏng lệch sóng là (k·2π + π) radian (trong cơ k là số nguyên) thì bọn chúng sẽ là ngược trộn.
Phân phỏng radian[sửa | sửa mã nguồn]
Các chi phí tố SI ví dụ như được sử dụng giới hạn với đơn vị chức năng rad muốn tạo rời khỏi phân phỏng radian; nhập toán học tập người tao ko sử dụng những số nhân (hay hay còn gọi là bội số) này.
Xem thêm: cách mở bài nghị luận xã hội
Trong một đàng tròn xoe với 2π × 1000 milliradian (≈ 6283,185 mrad). Vì vậy 1 milliradian lượng giác xấp xỉ 1⁄6283 đàng tròn xoe. Các căn nhà phát triển vũ khí coi phun dùng đơn vị chức năng này.
NATO và một số trong những tổ chức triển khai quân sự chiến lược dùng số lượng xấp xỉ với 1 milliradian lượng giác (0,001 rad) gọi là mil góc. 1 mil góc tương tự 1⁄6400 đàng tròn xoe và nhỏ rộng lớn 1-⅞% ví với một milliradian. Do sự tiện lợi vì thế số lượng 6400 mang đến khi cần thiết đo lường những góc nhỏ trong công việc coi súng nhưng mà người tao gật đầu bỏ dở sai số toán học tập nhỏ này. Trong quá khứ, những khối hệ thống pháo binh còn sử dụng những độ quý hiếm xấp xỉ với độ quý hiếm 1⁄2000π, ví dụ Thụy Điển sử dụng 1⁄6300 còn Liên Xô sử dụng 1⁄6000.
Trong thiên văn học tập, người tao với sử dụng những bội số nhỏ hơn hoàn toàn như microradian (μrad) và nanoradian (nrad). Độ phân kỳ của chùm tia laser cũng đo vị mrad hoặc bội số nhỏ hơn hoàn toàn như μrad và nrad.
Xem thêm[sửa | sửa mã nguồn]
- Tần số góc
- Gradian
- Phân tích điều hòa
- Steradian
- Lượng giác
Tham khảo[sửa | sửa mã nguồn]
- ^ Về những đơn vị chức năng đo lường và tính toán ko được dùng sau ngày 31/12/2005[liên kết hỏng], Tổng viên Tiêu chuẩn chỉnh Đo lường Chất lượng nước ta.
- ^ O'Connor, J. J.; Robertson, E. F. (tháng hai năm 2005). “Biography of Roger Cotes”. The MacTutor History of Mathematics. Bản gốc tàng trữ ngày 19 mon 10 năm 2012. Truy cập ngày 6 mon 9 năm 2013.
- ^ Luckey, Paul (1953) [Translation of 1424 book]. Siggel, A. (biên tập). Der Lehrbrief über den kreisumfang von Gamshid b. Mas'ud al-Kasi. Berlin: Akademie Verlag. tr. 40.
- ^ Cajori, Florian (1929). History of Mathematical Notations. 2. tr. 147–148. ISBN 0-486-67766-4.
- ^ Muir, Thos. (1910). “The Term "Radian" in Trigonometry”. Nature. 83 (2110): 156. Bibcode:1910Natur..83..156M. doi:10.1038/083156a0.Thomson, James (1910). “The Term "Radian" in Trigonometry”. Nature. 83 (2112): 217. Bibcode:1910Natur..83..217T. doi:10.1038/083217c0.Muir, Thos. (1910). “The Term "Radian" in Trigonometry”. Nature. 83 (2120): 459–460. Bibcode:1910Natur..83..459M. doi:10.1038/083459d0.
- ^ Miller, Jeff (23 mon 11 năm 2009). “Earliest Known Uses of Some of the Words of Mathematics”. Truy cập ngày 30 mon 9 năm 2011.
- ^ Xem tăng những nội dung bài viết sau để hiểu thêm: Brownstein, K. R. (1997). “Angles—Let's treat them squarely”. American Journal of Physics. 65 (7): 605. Bibcode:1997AmJPh..65..605B. doi:10.1119/1.18616., Romain, J.E. (1962). “Angles as a fourth fundamental quantity”. Journal of Research of the National Bureau of Standards-B. Mathematics and Mathematical Physics. 66B (3): 97., LéVy-Leblond, Jean-Marc (1998). “Dimensional angles and universal constants”. American Journal of Physics. 66 (9): 814. Bibcode:1998AmJPh..66..814L. doi:10.1119/1.18964., and Romer, Robert H. (1999). “Units—SI-Only, or Multicultural Diversity?”. American Journal of Physics. 67: 13. Bibcode:1999AmJPh..67...13R. doi:10.1119/1.19185.

















































Bình luận